There is a long tradition in conventional urban geography of measuring the hinterlands of towns and cities. The concept of hinterworld was created to describe the worldwide pattern of connections between a given world city and other world cities under conditions of contemporary globalisation.
The concept was introduced by Peter J. Taylor in GaWC Research Bulletin 17 and is refined in Research Bulletin 89. Examples of its use can be found in Research Bulletin 58. The maps in this atlas are all based on the methodology presented in Research Bulletin 89 using the city/global service firms data for 2000 described in Research Bulletin 43.
References
RB 17: Taylor, P.J. (2001) Urban hinterworlds: geographies of corporate service provision under conditions of contemporary globalisation, Geography, 86 (1), 51-60.
RB 89: Taylor, P.J. and Walker, D.R.F. (2004) Urban hinterworlds revisited, Geography, 89 (2), 145-151.
RB 58: Taylor, P.J. (2001) West Asian/North African cities in the world city network: a global analysis of dependence, integration and autonomy, The Arab World Geographer, 4 (3), 146-159.
RB 43: Taylor, P.J., Catalano, G. and Walker, D.R.F. (2002) Measurement of the world city network, Urban Studies, 39 (13), 2367-2376.
Method
In summary the method is as follows:
- We have selected the top 123 cities in terms of global network connectivity and measure the connectivity between each city and the other 122 cities.
- These individual city inter-linkages closely reflect the overall pattern of global network connectivity (i.e. every city is most connected to either London or New York).
- For each city we regress its connectivities with other cities against their global network connectivity.
- We compute the residuals from the regression line and these are interpreted as a city being either over-linked (positive residuals) to another city (relative to its global network connectivity) or under-linked (negative residuals). It is these residuals that are mapped to show a city’s hinterworld.
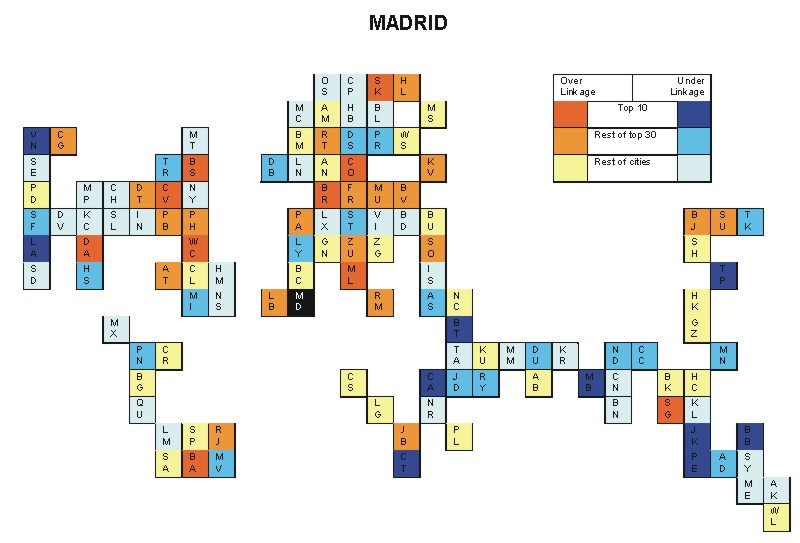
- The standard error of estimate indicates how close the scatter of points is to the line: it is interpreted in this context of indicating the specificity of a city’s hinterworld (i.e. zero would indicate a hinterworld exactly the same as the global network connectivity pattern and therefore the higher the standard error the more unlike a city’s hinterworld is from the general pattern of global connectivities. In the analyses, standard errors range from 0.013 (Madrid) to 0.067 (Indianapolis)).
- The same ordinal scale is used for all maps to facilitate simple comparisons between hinterworlds. An initial discussion of comparisons can be found in chapter 5 of P.J. Taylor (2004) World City Network: A Global Urban Analysis (London: Routledge).
- The maps are in cartogram form, which places cities in their approximate relative geographical positions (city codes are listed at the bottom of this page).
Atlas maps
The result is an atlas containing maps of hinterworlds for 123 cities in the year 2000. These are presented alphabetically below. The cities most and least linked to a given city are listed along with the measure of specificity.
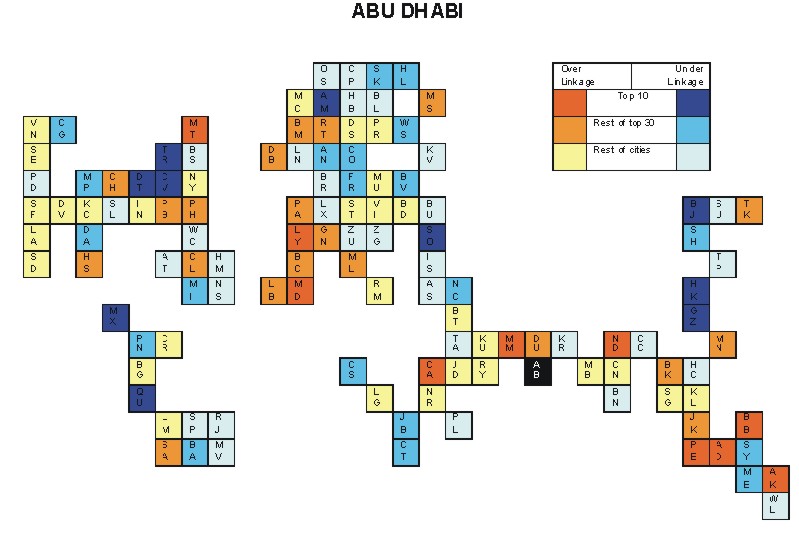
Most over-linked city: Auckland (0.103)
Most under-linked city: Detroit (-0.084)
Specificity of hinterworld: 0.031
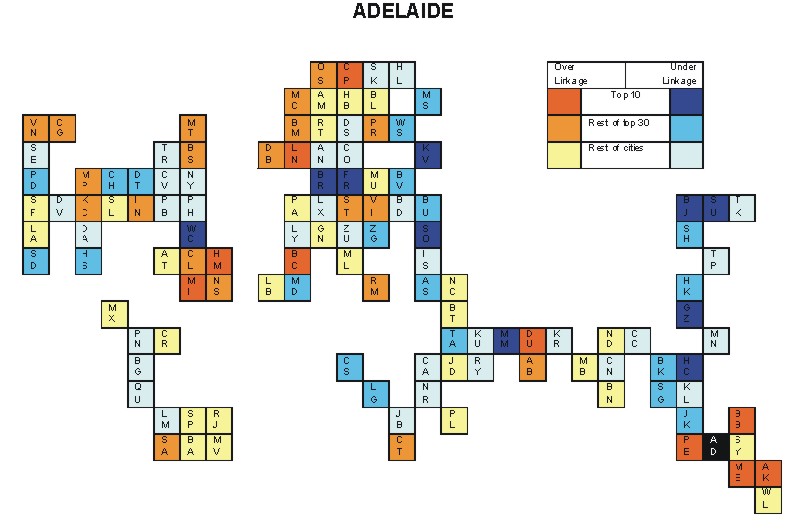
Most over-linked city: Perth (0.171)
Most under-linked city: Sofia (-0.087)
Specificity of hinterworld: 0.043
Most over-linked city: Beijing (0.048)
Most under-linked city: Los Angeles (-0.043)
Specificity of hinterworld: 0.017

Most over-linked city: Cologne (0.112)
Most under-linked city: Taipei (-0.077)
Specificity of hinterworld: 0.034
Most over-linked city: Istanbul (0.080)
Most under-linked city: Boston (-0.098)
Specificity of hinterworld: 0.034

Most over-linked city: Boston (0.110)
Most under-linked city: Athens (-0.046)
Specificity of hinterworld: 0.027

Most over-linked city: Montreal (0.046)
Most under-linked city: Luxembourg City (-0.056)
Specificity of hinterworld: 0.017
Most over-linked city: New Delhi (0.122)
Most under-linked city: Boston (-0.105)
Specificity of hinterworld: 0.033
Most over-linked city: Tokyo (0.058)
Most under-linked city: Toronto (-0.056)
Specificity of hinterworld: 0.022
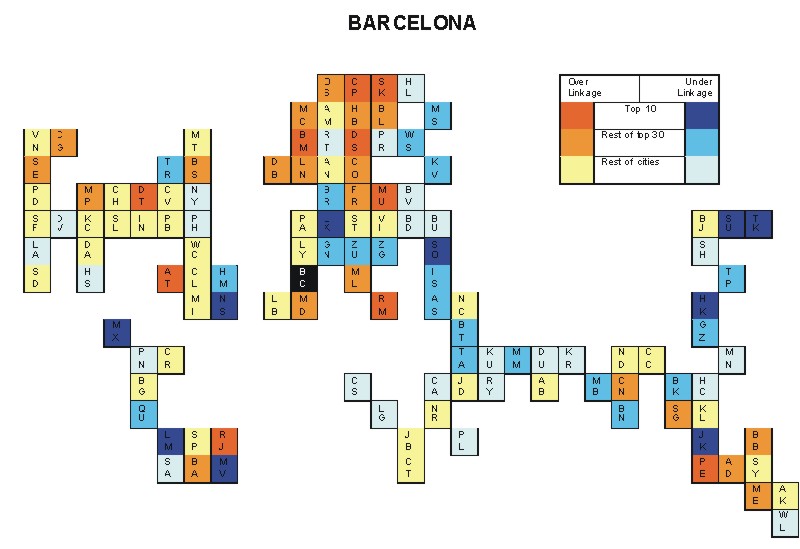
Most over-linked city: Rome (0.034)
Most under-linked city: Lima (-0.045)
Specificity of hinterworld: 0.017
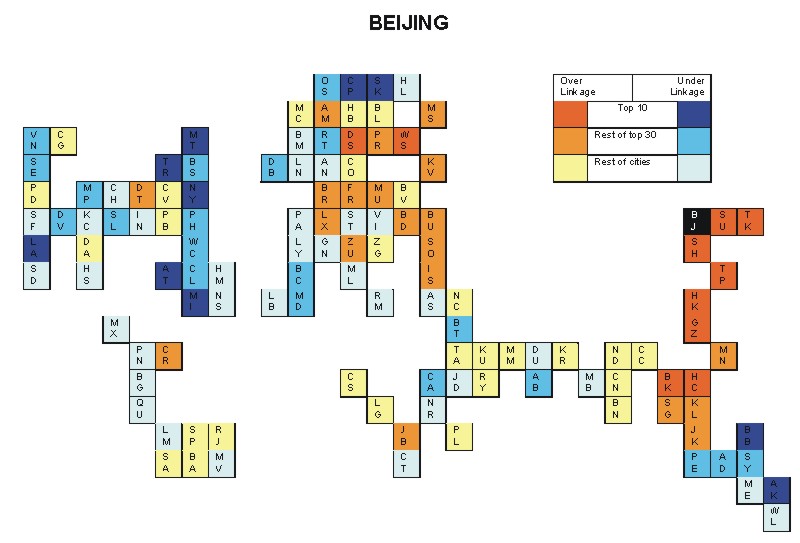
Most over-linked city: Guangzhou (0.071)
Most under-linked city: Montreal (-0.051)
Specificity of hinterworld: 0.025
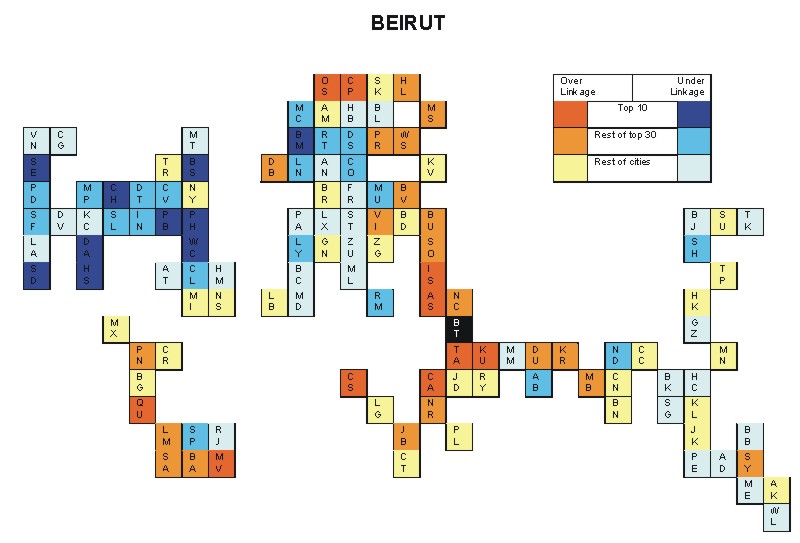
Most over-linked city: Athens (0.076)
Most under-linked city: Washington, DC (-0.086)
Specificity of hinterworld: 0.034
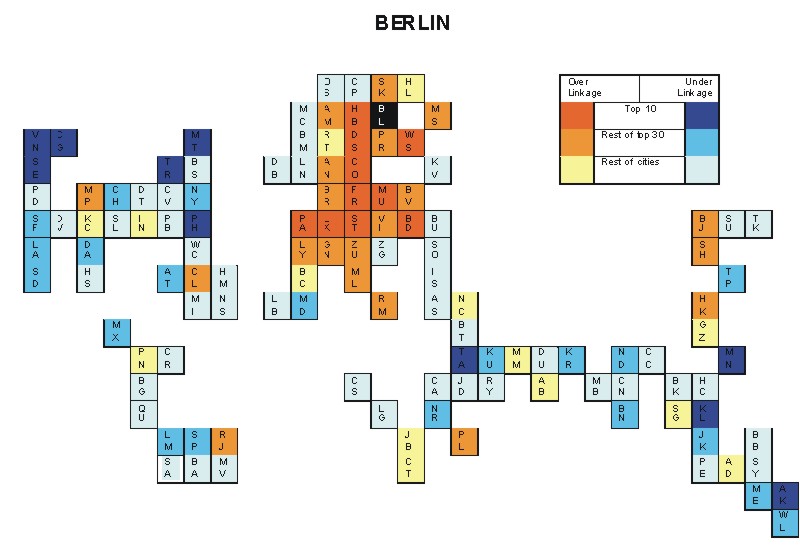
Most over-linked city: Munich (0.168)
Most under-linked city: Toronto (-0.108)
Specificity of hinterworld: 0.040
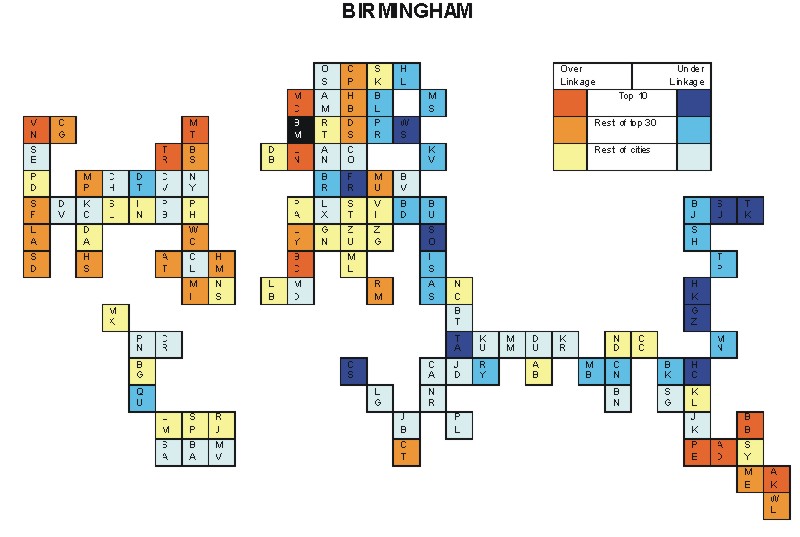
Most over-linked city: Manchester (0.137)
Most under-linked city: Tokyo (-0.092)
Specificity of hinterworld: 0.046
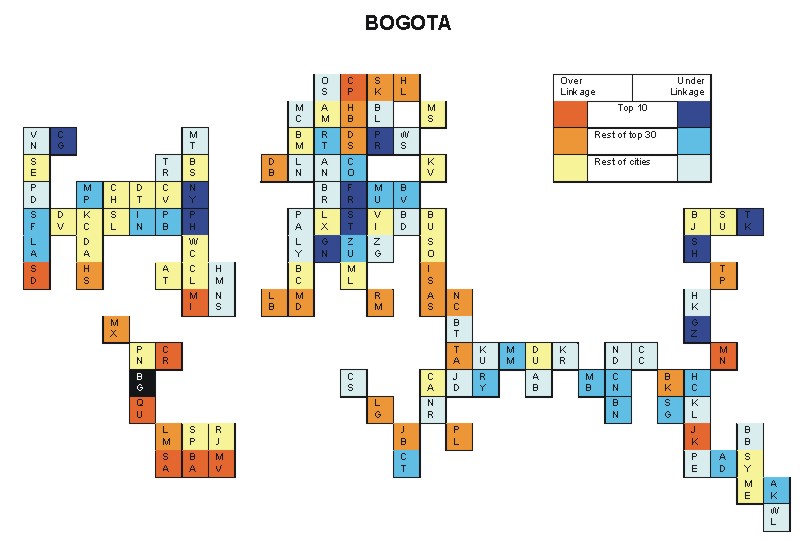
Most over-linked city: Caracas (0.067)
Most under-linked city: Stuttgart (-0.034)
Specificity of hinterworld: 0.018
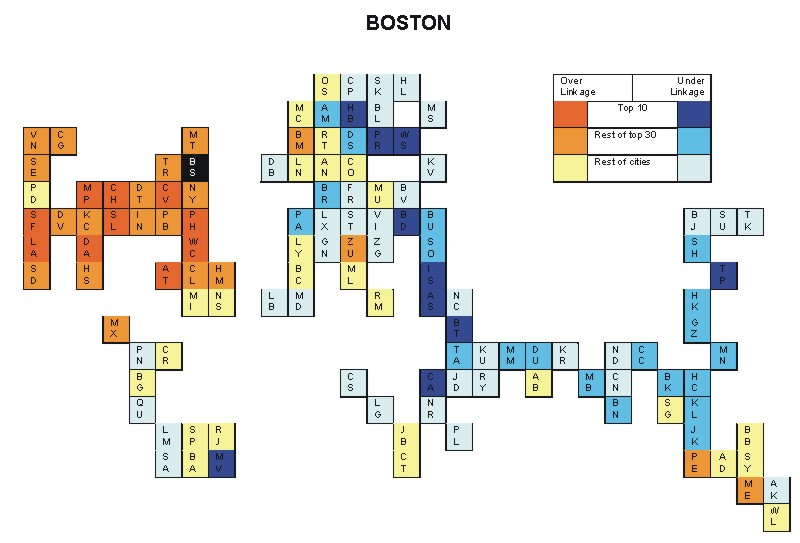
Most over-linked city: Washington, DC (0.125)
Most under-linked city: Athens (-0.092)
Specificity of hinterworld: 0.045
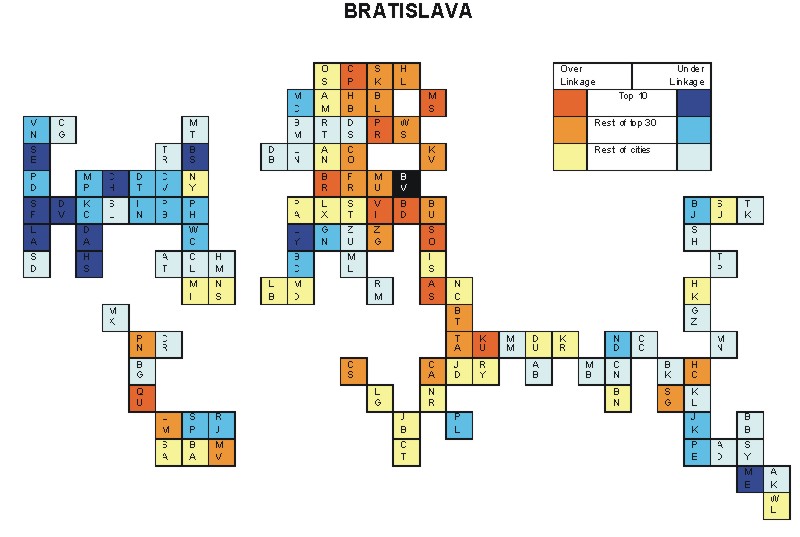
Most over-linked city: Prague (0.102)
Most under-linked city: Chicago (-0.106)
Specificity of hinterworld: 0.043
Most over-linked city: Perth (0.122)
Most under-linked city: Frankfurt (-0.101)
Specificity of hinterworld: 0.036

Most over-linked city: Frankfurt (0.038)
Most under-linked city: Toronto (-0.032)
Specificity of hinterworld: 0.014

Most over-linked city: Johannesburg (0.109)
Most under-linked city: Washington, DC (-0.108)
Specificity of hinterworld: 0.048
Most over-linked city: Prague (0.097)
Most under-linked city: Los Angeles (-0.075)
Specificity of hinterworld: 0.031
Most over-linked city: Caracas (0.059)
Most under-linked city: Seattle (-0.039)
Specificity of hinterworld: 0.015
Most over-linked city: Beirut (0.068)
Most under-linked city: Washington, DC (-0.088)
Specificity of hinterworld: 0.030
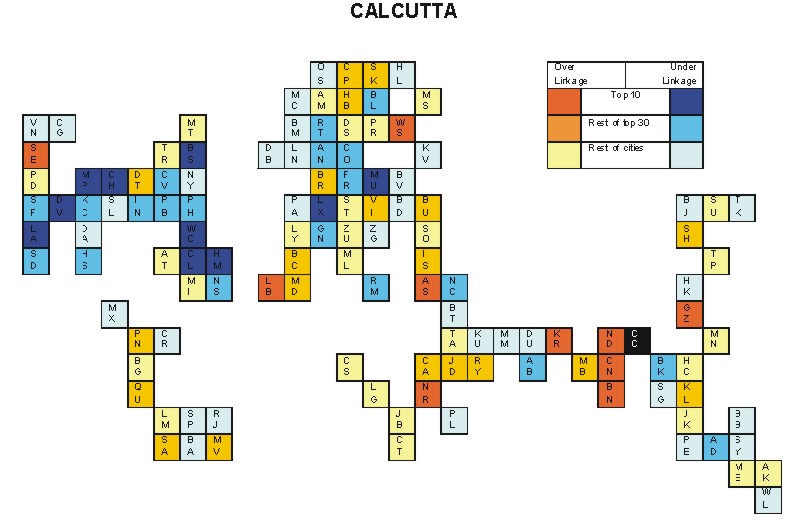
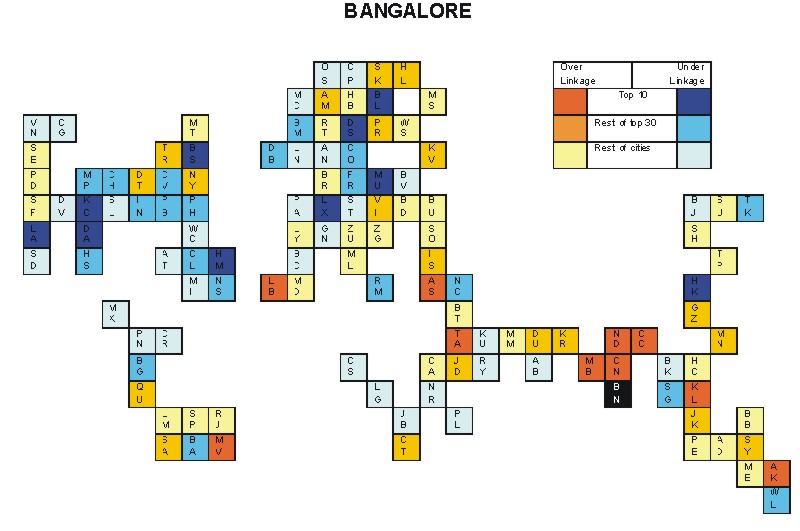
Most over-linked city: Chennai (0.103)
Most under-linked city: Chicago (-0.093)
Specificity of hinterworld: 0.036

Most over-linked city: Montreal (0.129)
Most under-linked city: Luxembourg (-0.105)
Specificity of hinterworld: 0.045
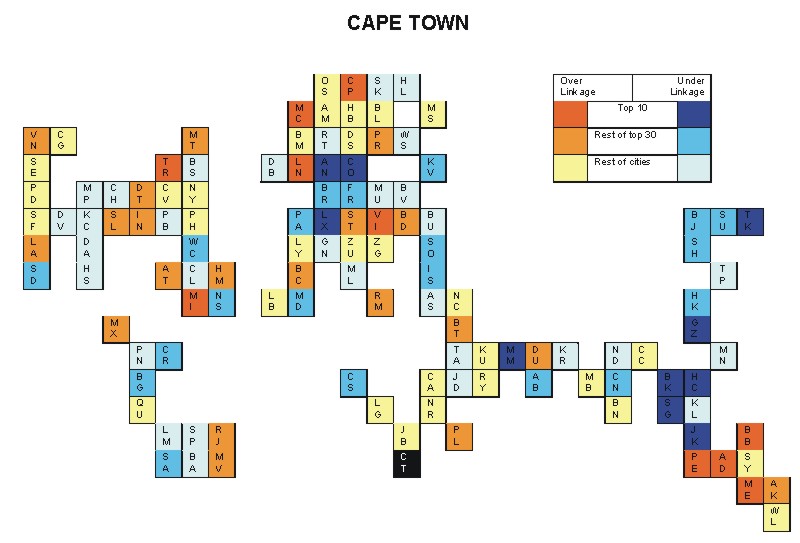
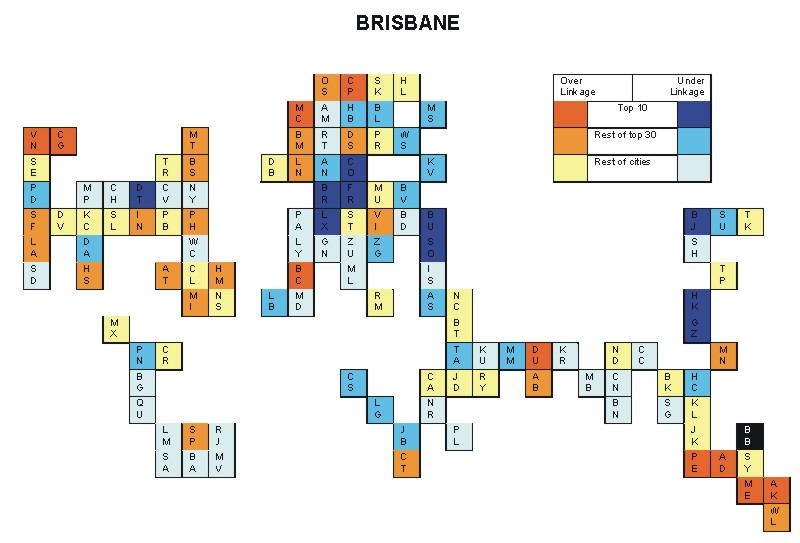
Most over-linked city: Brisbane (0.073)
Most under-linked city: Ho Chi Minh City (-0.074)
Specificity of hinterworld: 0.035
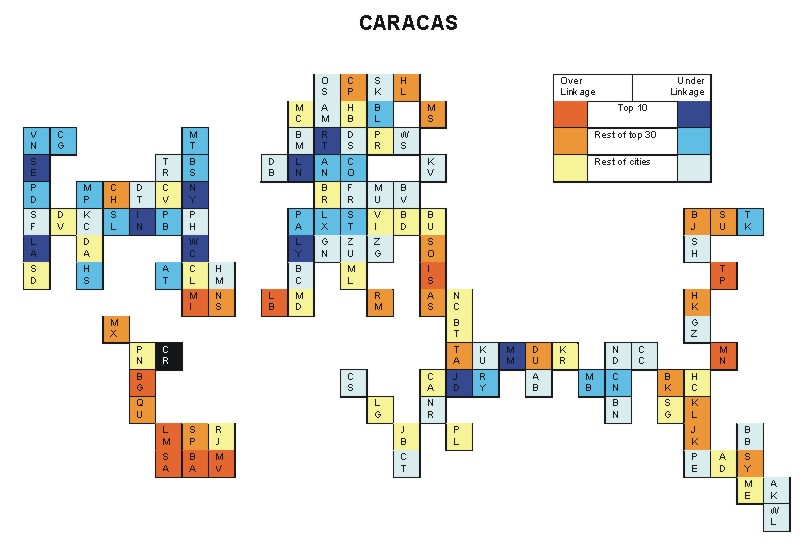
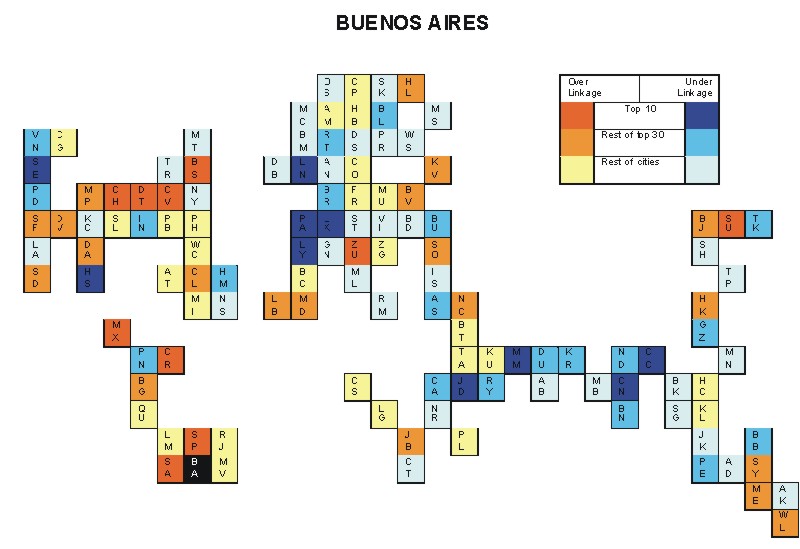
Most over-linked city: Buenos Aires (0.086)
Most under-linked city: New York (-0.045)
Specificity of hinterworld: 0.020

Most over-linked city: Tel Aviv (0.126)
Most under-linked city: Boston (-0.102)
Specificity of hinterworld: 0.050
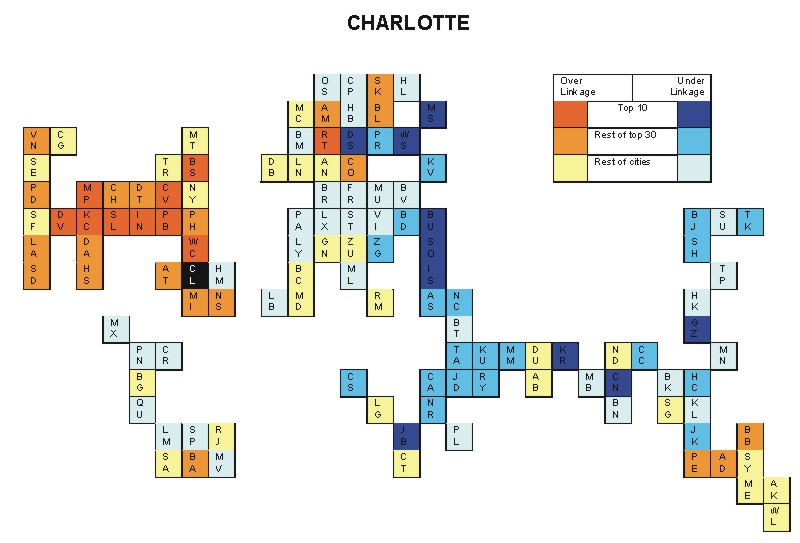
Most over-linked city: Minneapolis (0.169)
Most under-linked city: Warsaw (-0.131)
Specificity of hinterworld: 0.060
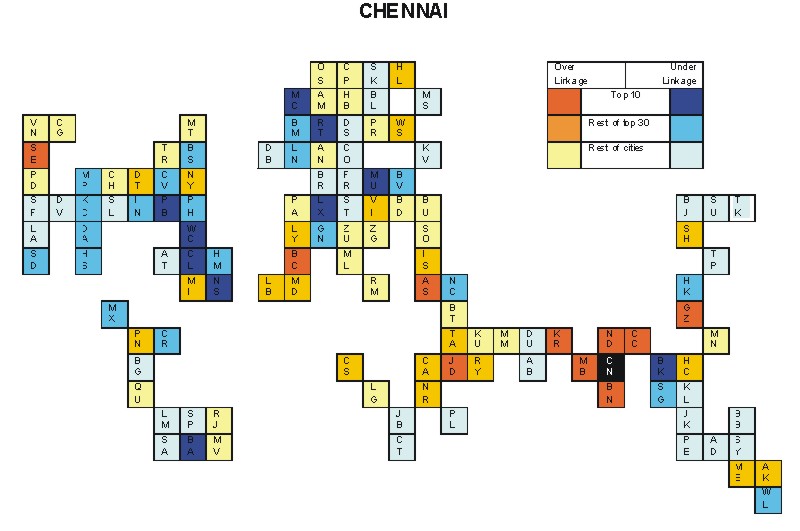
Most over-linked city: Calcutta (0.103)
Most under-linked city: Charlotte (-0.093)
Specificity of hinterworld: 0.041
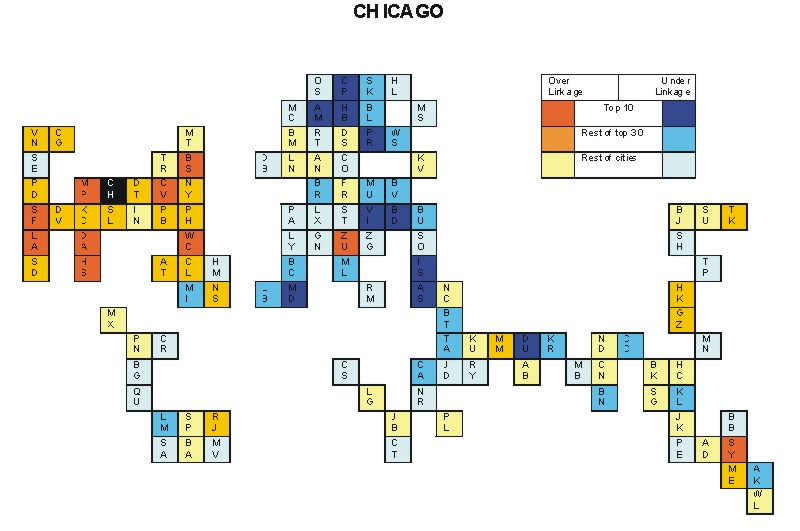
Most over-linked city: Boston (0.066)
Most under-linked city: Budapest (-0.038)
Specificity of hinterworld: 0.019
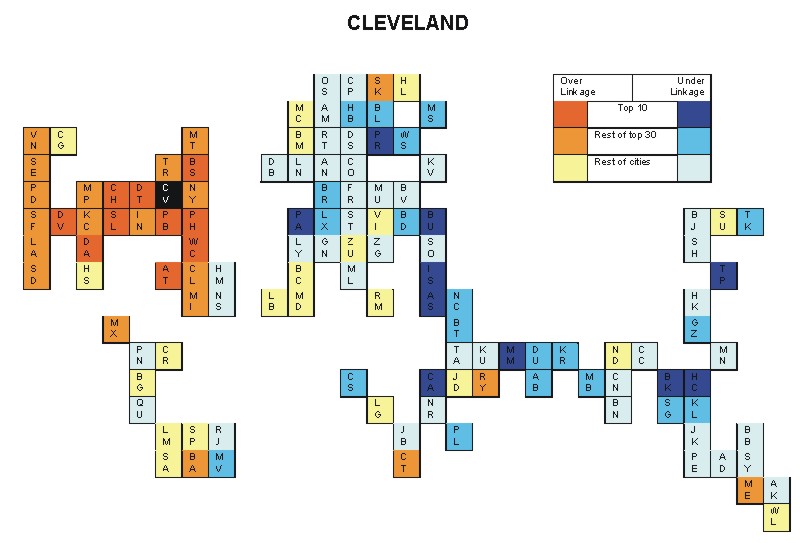
Most over-linked city: Washington, DC (0.192)
Most under-linked city: Manama (-0.104)
Specificity of hinterworld: 0.059
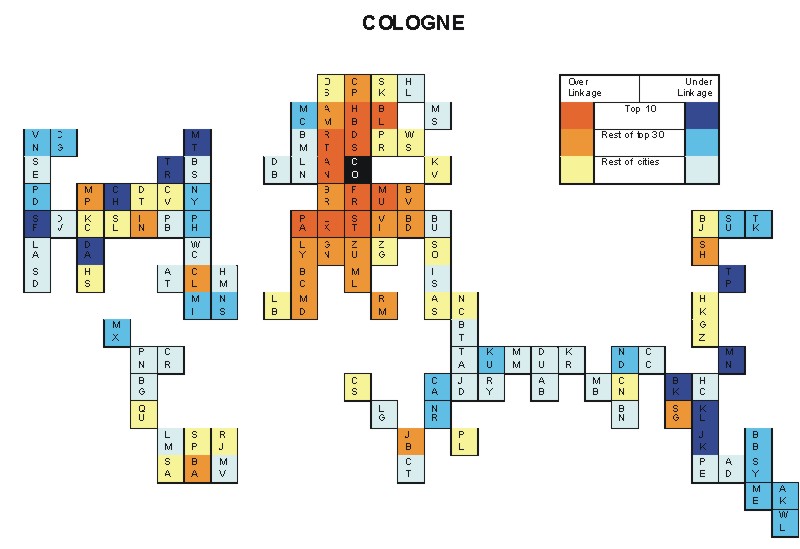
Most over-linked city: Munich (0.159)
Most under-linked city: Manila (-0.083)
Specificity of hinterworld: 0.049

Most over-linked city: Helsinki (0.072)
Most under-linked city: Manama (-0.063)
Specificity of hinterworld: 0.025
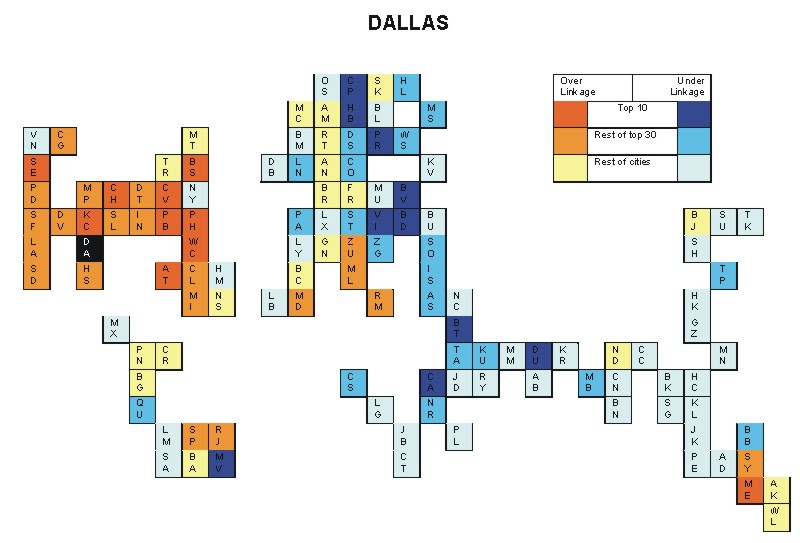
Most over-linked city: Chicago (0.114)
Most under-linked city: Beirut (-0.064)
Specificity of hinterworld: 0.045

Most over-linked city: Washington, DC (0.144)
Most under-linked city: Warsaw (-0.096)
Specificity of hinterworld: 0.047
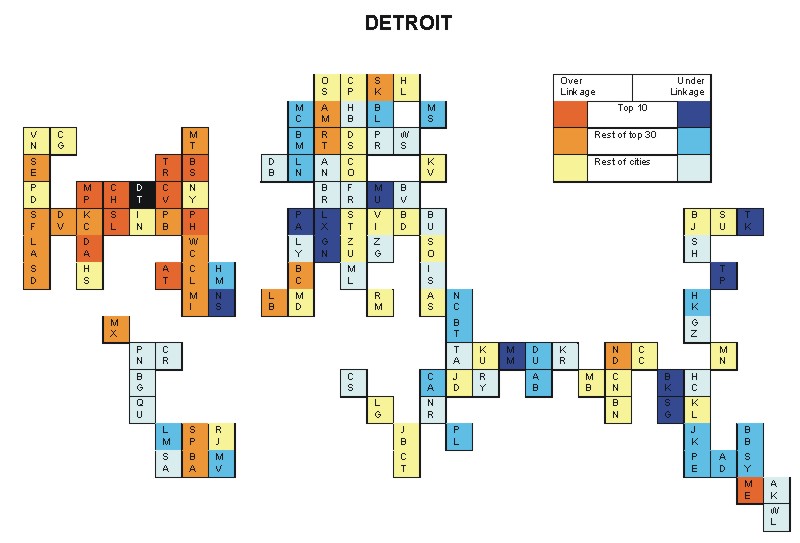
Most over-linked city: Cleveland (0.104)
Most under-linked city: Nassau (-0.079)
Specificity of hinterworld: 0.039
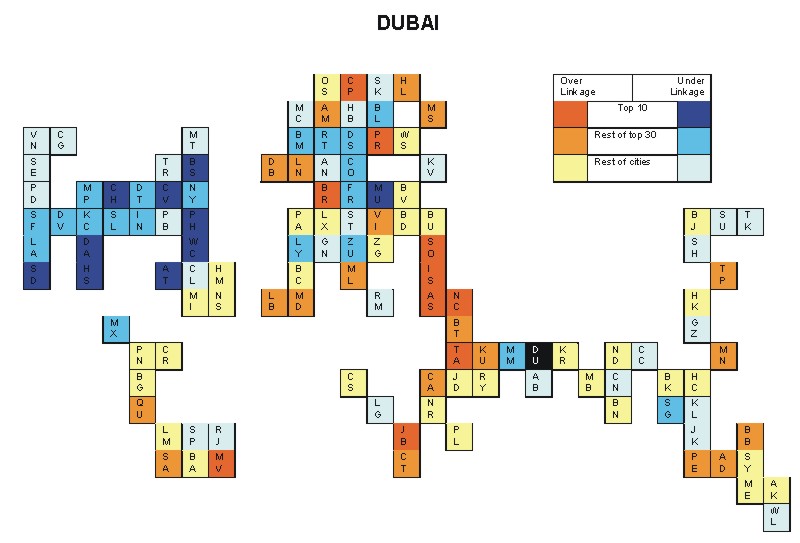
Most over-linked city: Prague (0.065)
Most under-linked city: Washington, DC (-0.100)
Specificity of hinterworld: 0.026
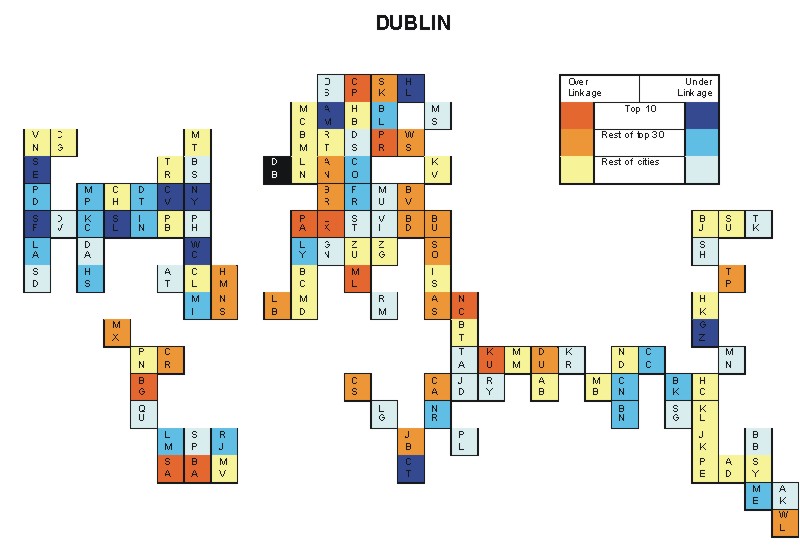
Most over-linked city: Milan (0.035)
Most under-linked city: Washington, DC (-0.065)
Specificity of hinterworld: 0.016
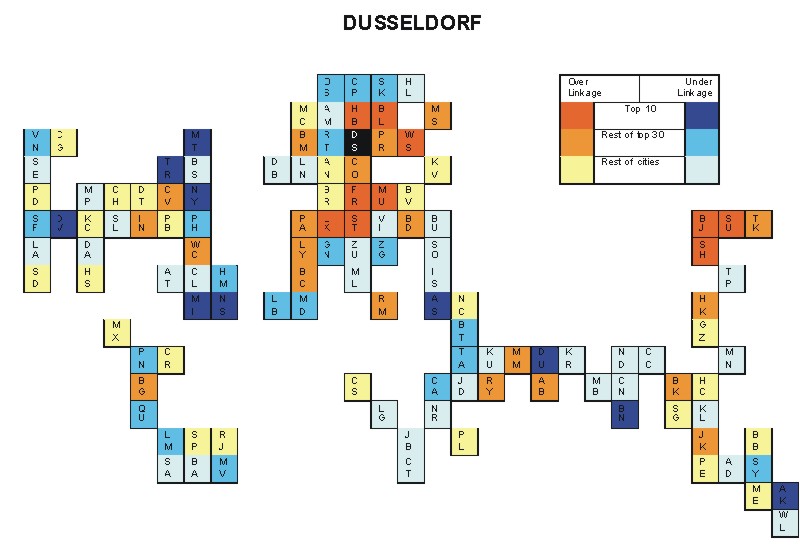
Most over-linked city: Munich (0.115)
Most under-linked city: New York (-0.056)
Specificity of hinterworld: 0.030
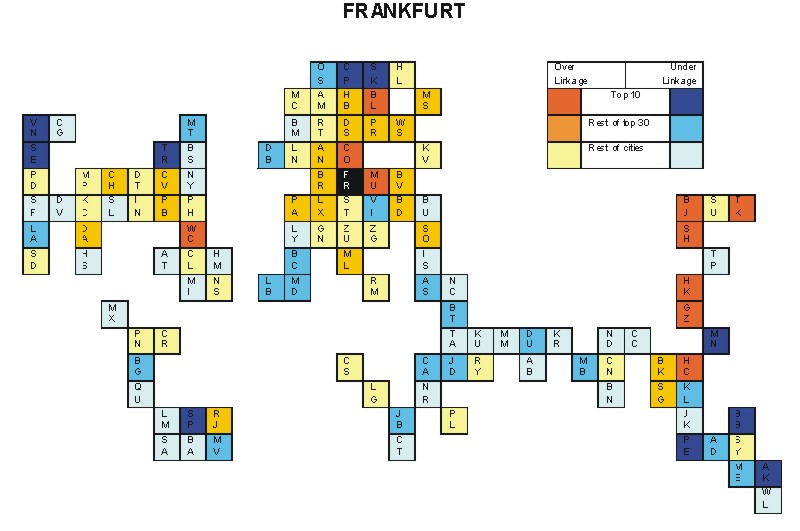
Most over-linked city: Washington, DC (0.072)
Most under-linked city: Toronto (-0.057)
Specificity of hinterworld: 0.022
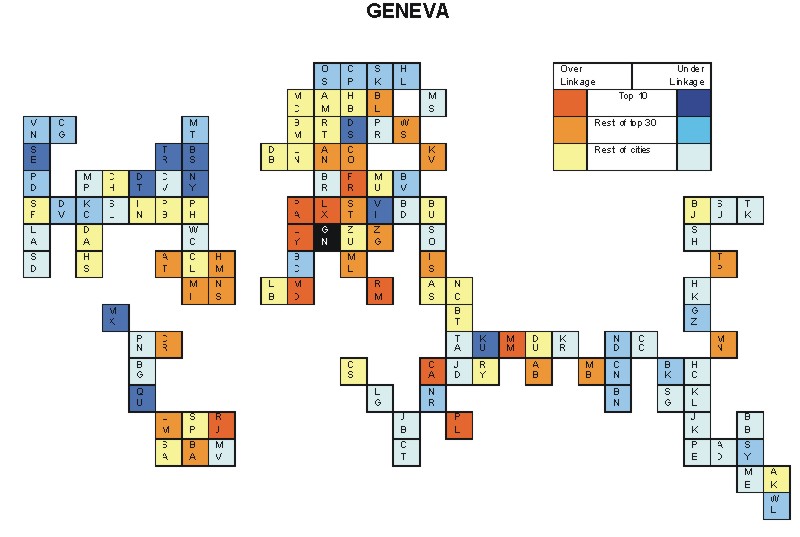
Most over-linked city: Rio de Janeiro (0.072)
Most under-linked city: Toronto (-0.049)
Specificity of hinterworld: 0.022
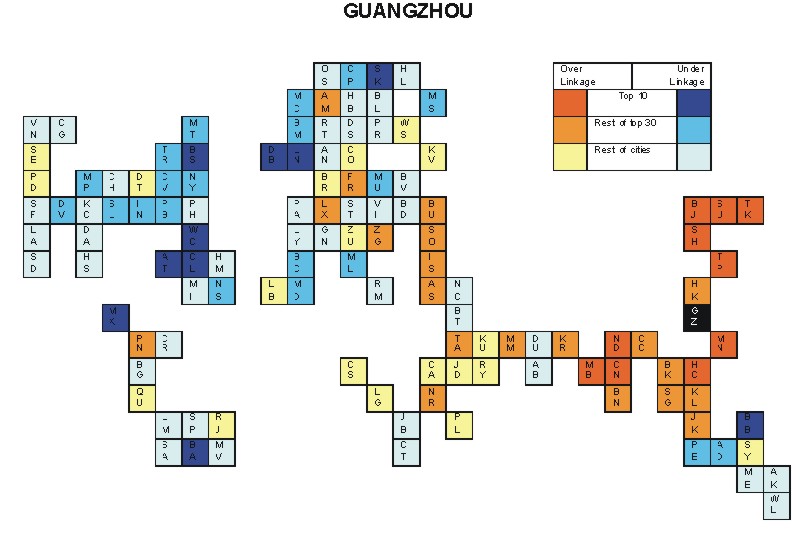
Most over-linked city: Ho Chi Minh City (0.171)
Most under-linked city: Washington, DC (-0.125)
Specificity of hinterworld: 0.051
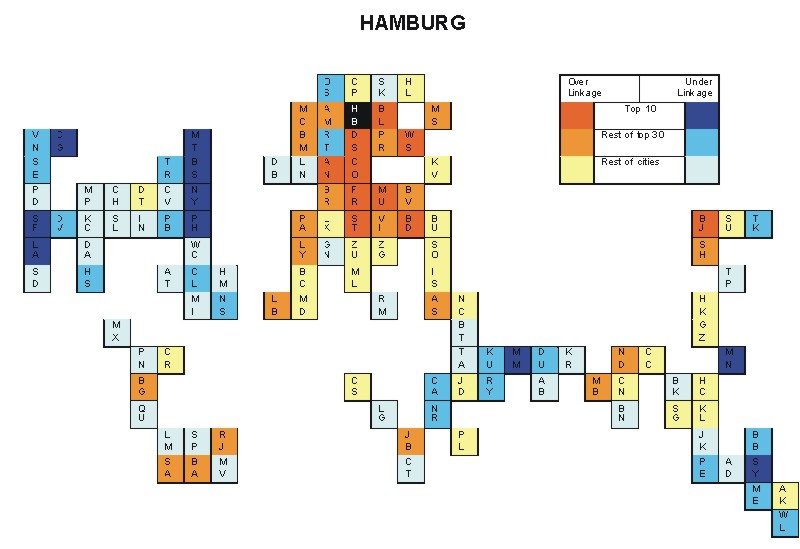
Most over-linked city: Munich (0.128)
Most under-linked city: New York (-0.065)
Specificity of hinterworld: 0.030
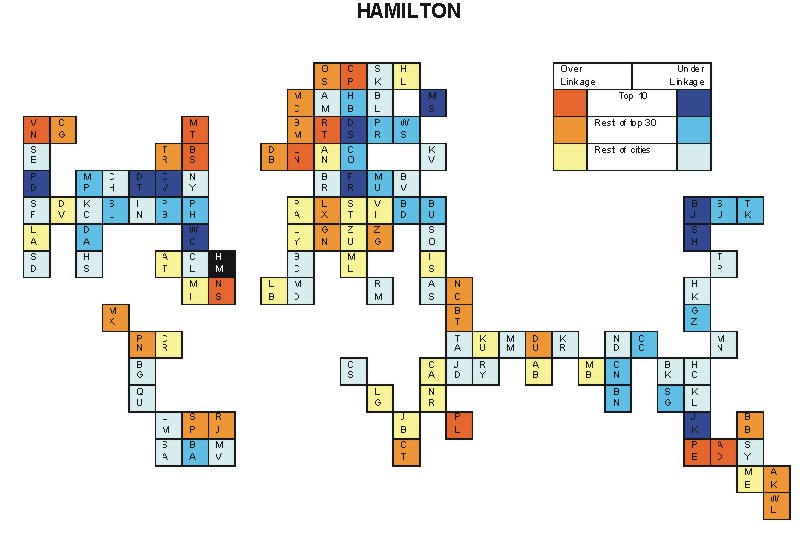
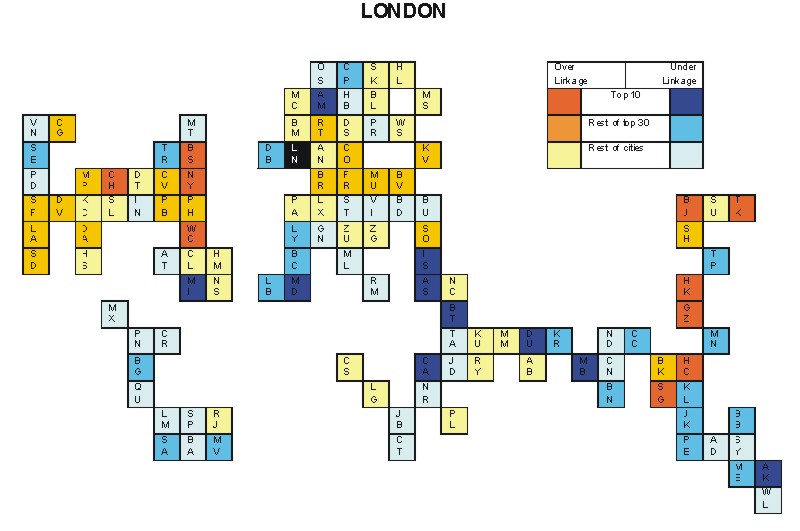
Most over-linked city: London (0.116)
Most under-linked city: Frankfurt (-0.076)
Specificity of hinterworld: 0.038
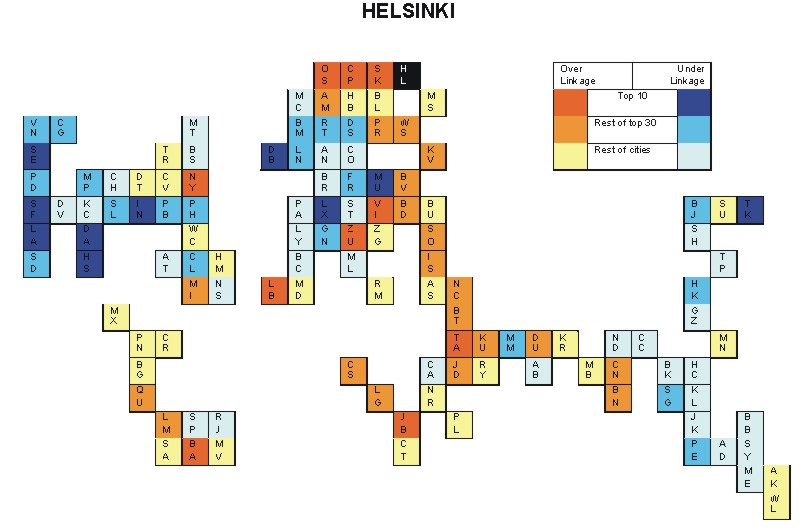
Most over-linked city: Copenhagen (0.101)
Most under-linked city: Luxembourg City (-0.069)
Specificity of hinterworld: 0.036

Most over-linked city: Guangzhou (0.141)
Most under-linked city: Washington, DC (-0.099)
Specificity of hinterworld: 0.042

Most over-linked city: Beijing (0.049)
Most under-linked city: Auckland (-0.040)
Specificity of hinterworld: 0.018
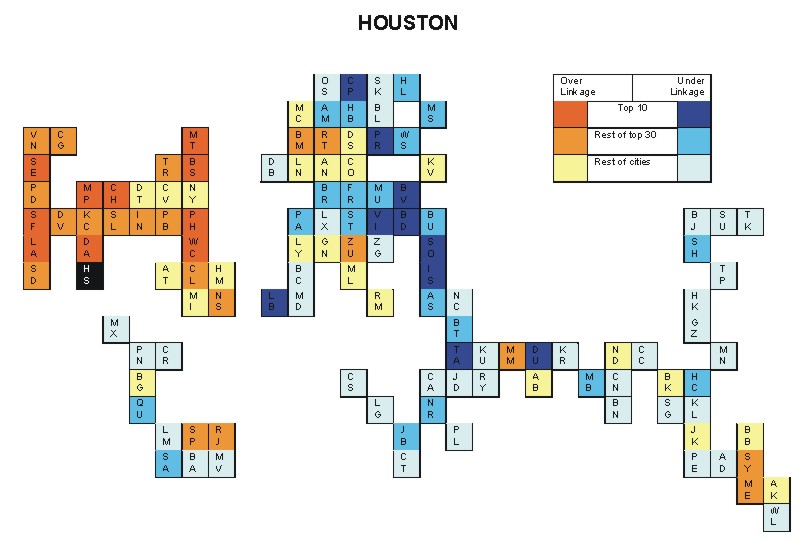
Most over-linked city: San Francisco (0.076)
Most under-linked city: Prague (-0.054)
Specificity of hinterworld: 0.031
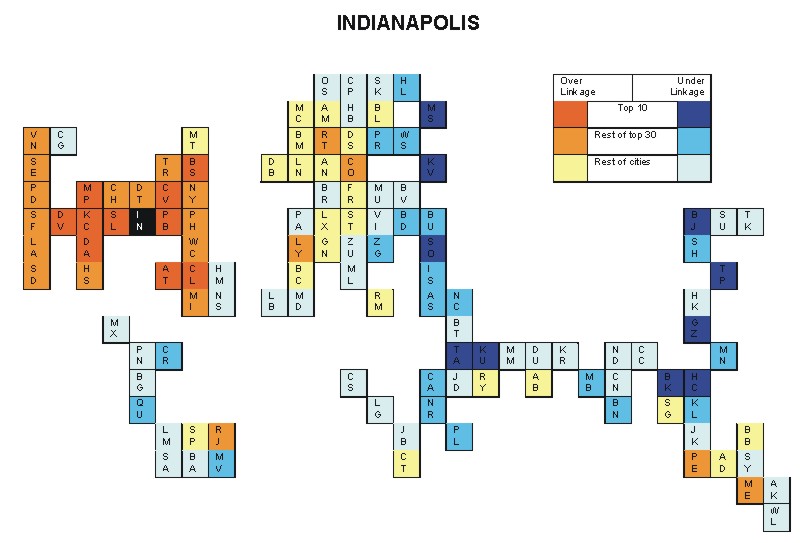
Most over-linked city: Minneapolis (0.183)
Most under-linked city: Sofia (-0.125)
Specificity of hinterworld: 0.067

Most over-linked city: Johannesburg (0.063)
Most under-linked city: Boston (-0.060)
Specificity of hinterworld: 0.029
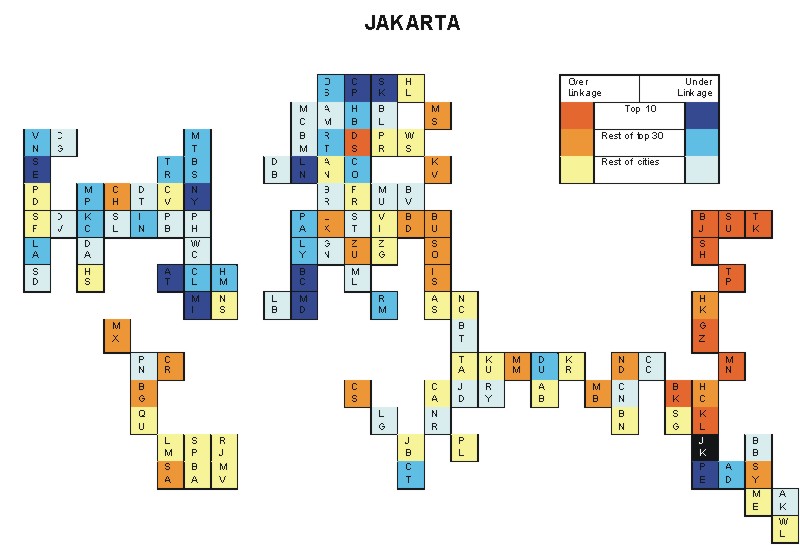
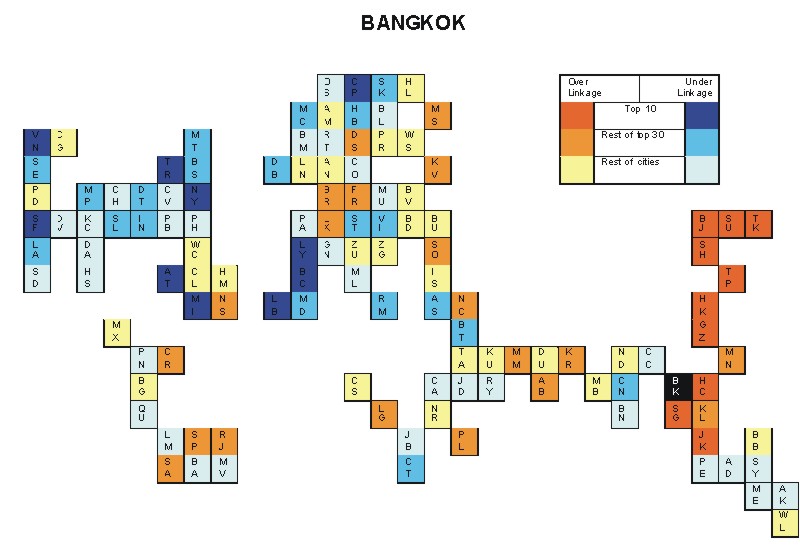
Most over-linked city: Bangkok (0.072)
Most under-linked city: Miami (-0.047)
Specificity of hinterworld: 0.021
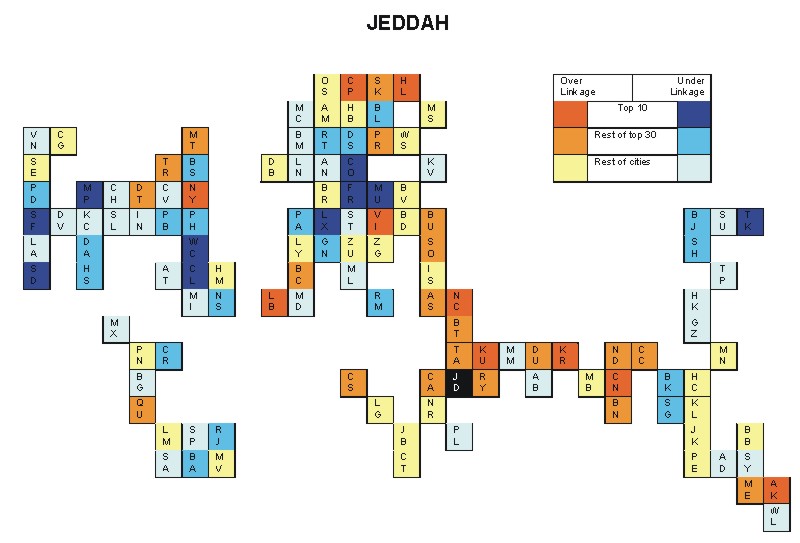
Most over-linked city: New York (0.114)
Most under-linked city: Frankfurt (-0.097)
Specificity of hinterworld: 0.036
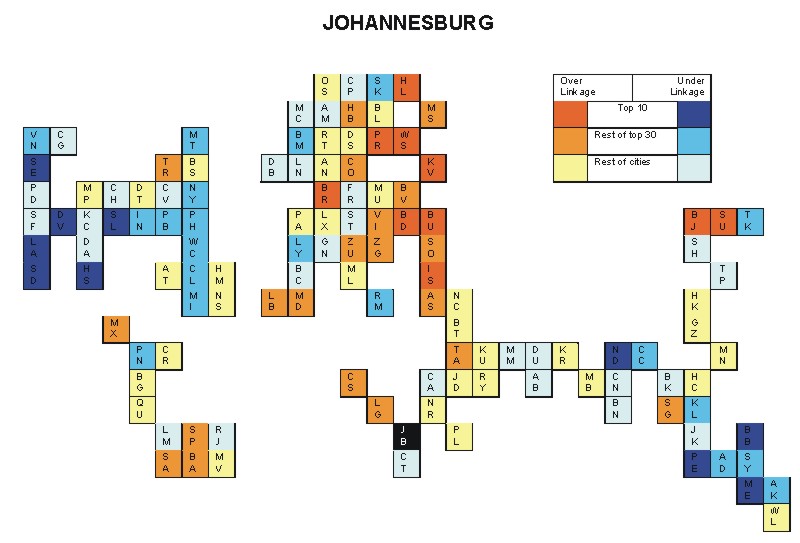
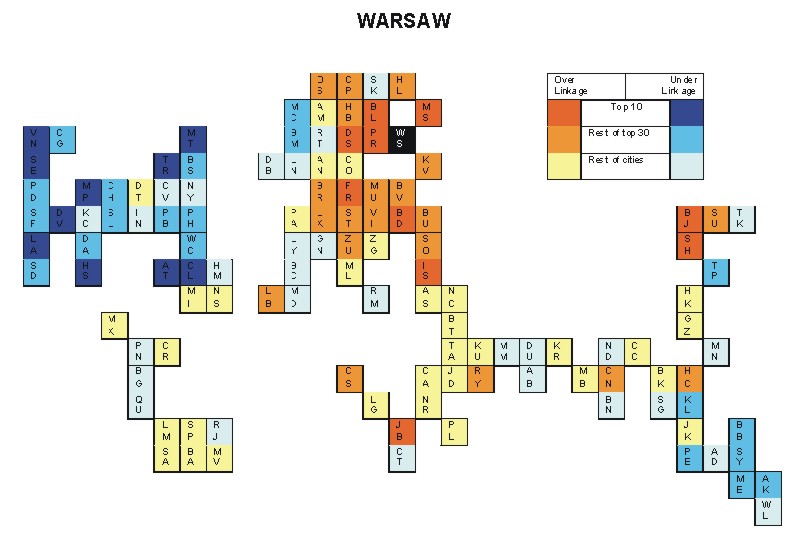
Most over-linked city: Warsaw (0.058)
Most under-linked city: Denver (-0.043)
Specificity of hinterworld: 0.021
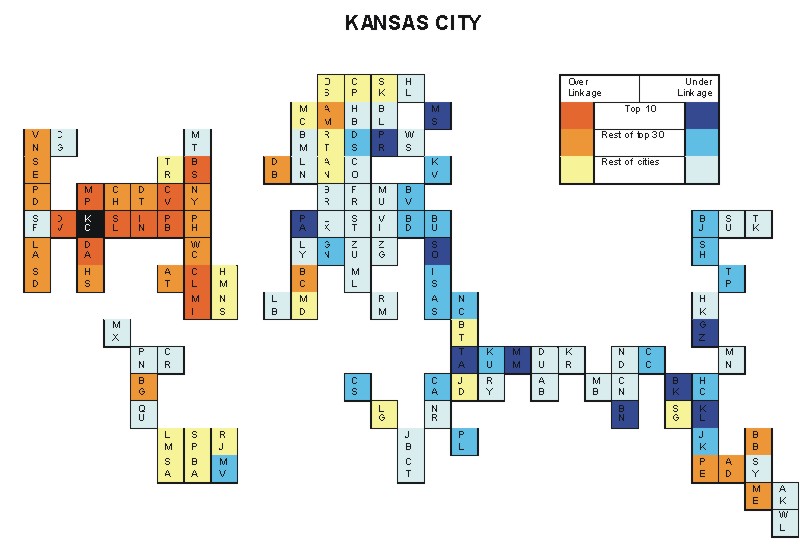
Most over-linked city: Dallas (0.162)
Most under-linked city: Manama (-0.090)
Specificity of hinterworld: 0.054
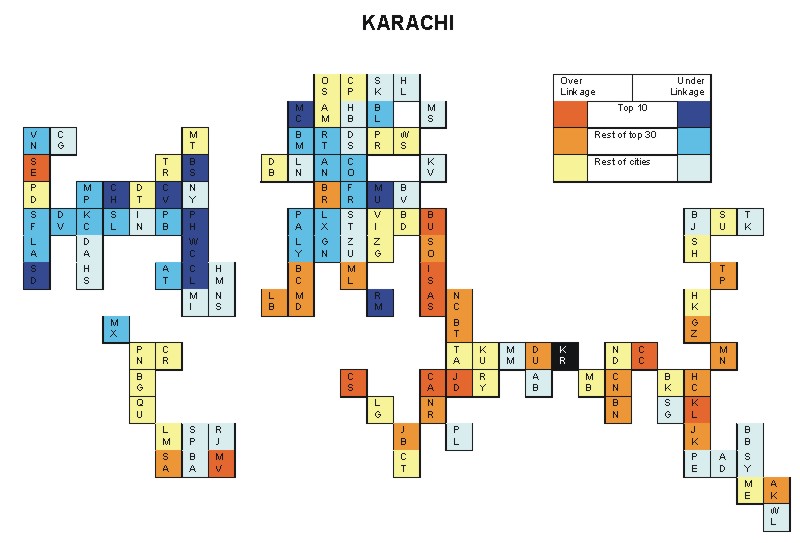
Most over-linked city: Bucharest (0.095)
Most under-linked city: Washington, DC (-0.108)
Specificity of hinterworld: 0.038
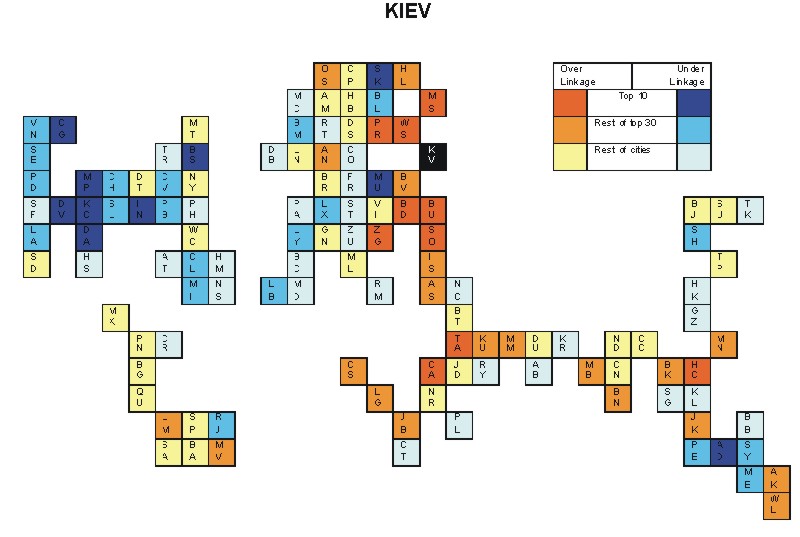
Most over-linked city: Warsaw (0.089)
Most under-linked city: Boston (-0.099)
Specificity of hinterworld: 0.038
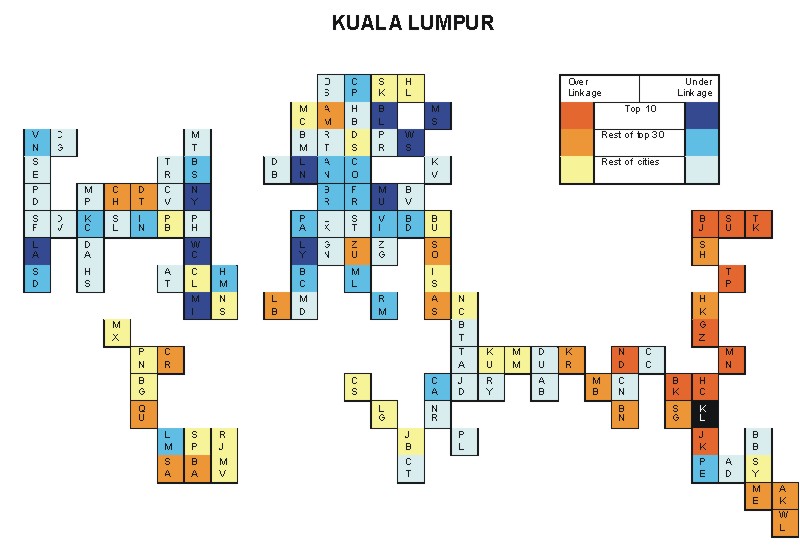
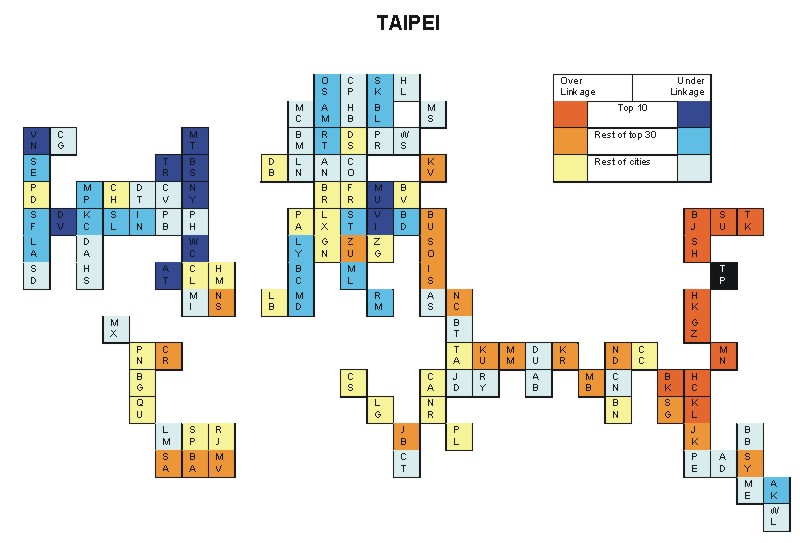
Most over-linked city: Taipei (0.060)
Most under-linked city: New York (-0.056)
Specificity of hinterworld: 0.021
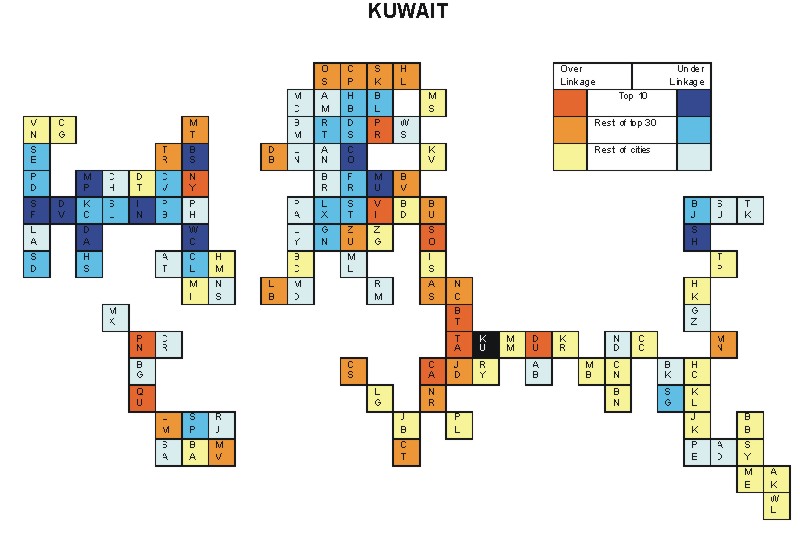
Most over-linked city: Tel Aviv (0.108)
Most under-linked city: Washington, DC (-0.127)
Specificity of hinterworld: 0.053
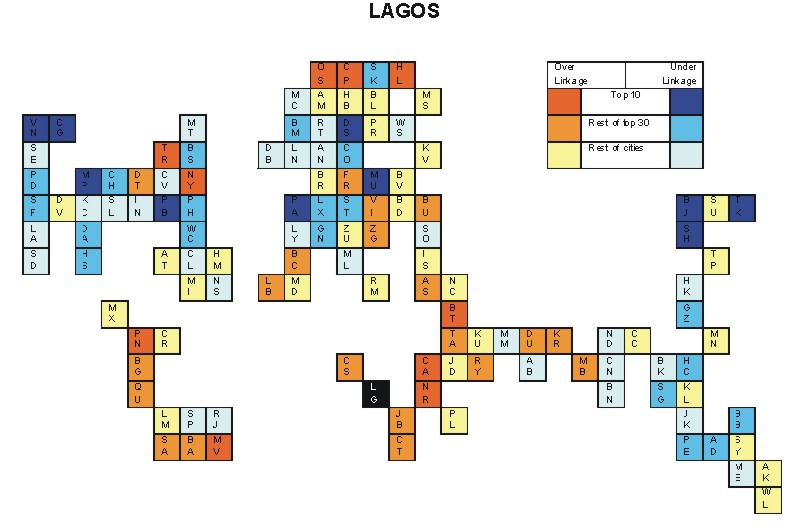
Most over-linked city: Nairobi (0.090)
Most under-linked city: Paris (-0.084)
Specificity of hinterworld: 0.017
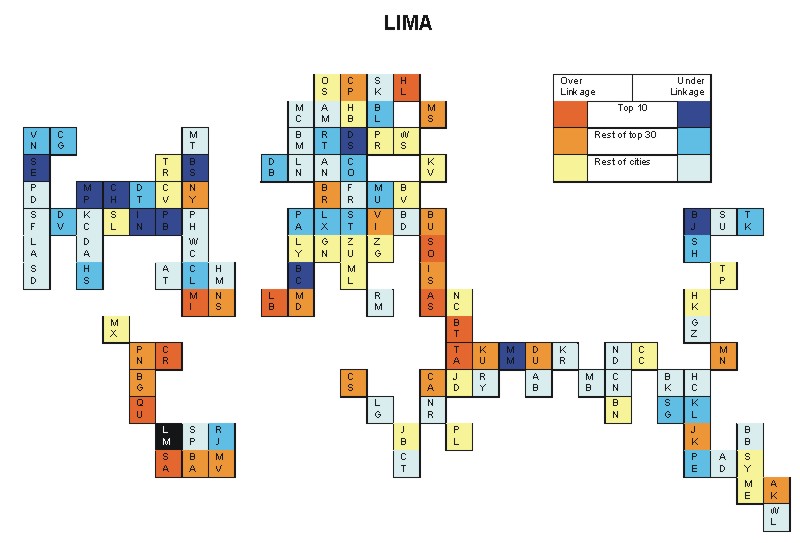
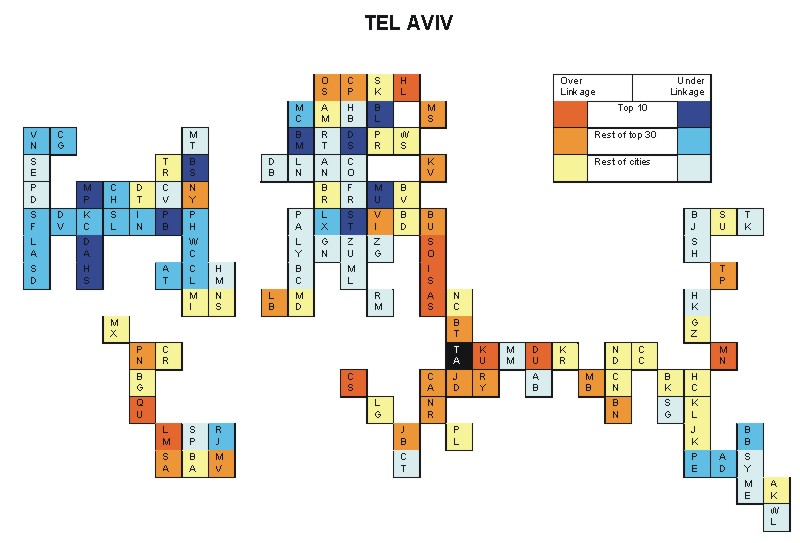
Most over-linked city: Tel Aviv (0.192)
Most under-linked city: Boston (-0.084)
Specificity of hinterworld: 0.036
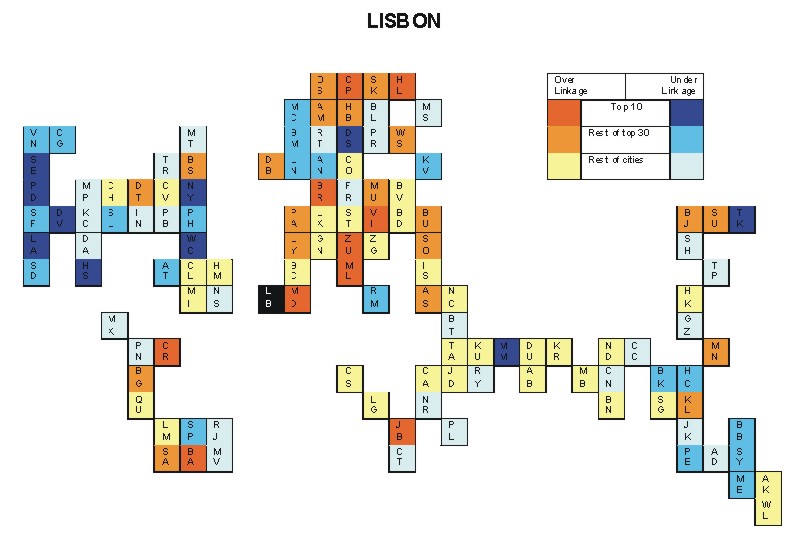
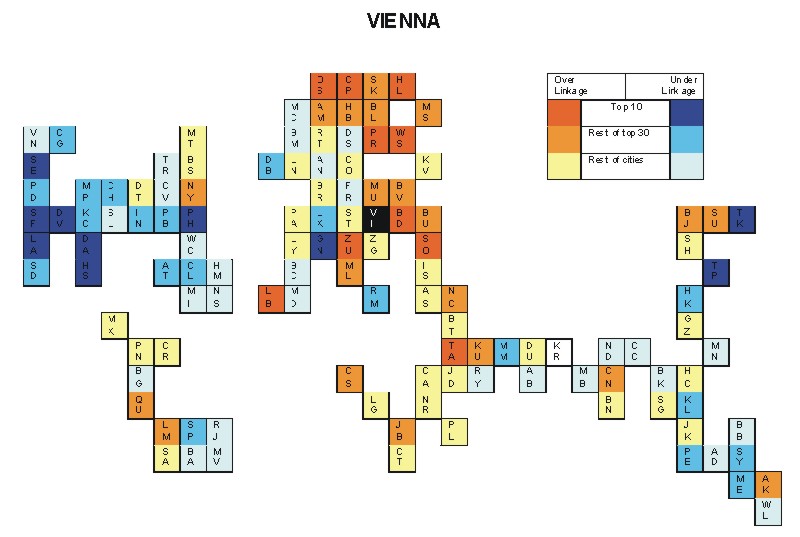
Most over-linked city: Vienna (0.039)
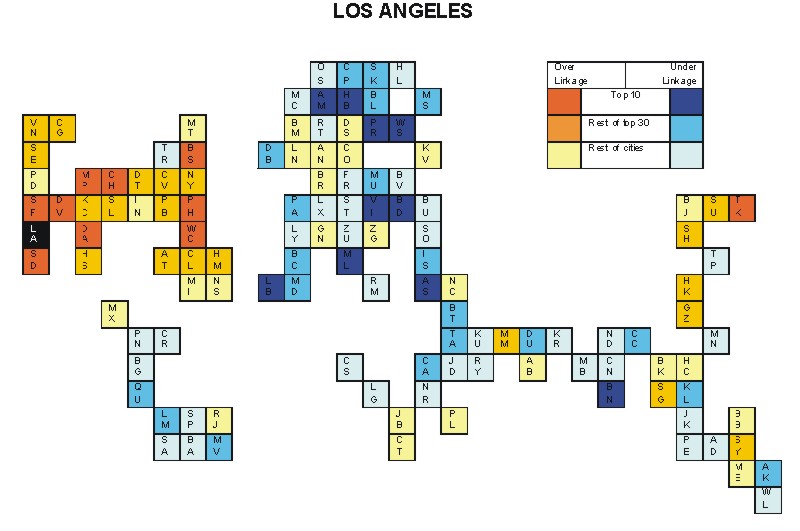
Most under-linked city: Los Angeles (-0.049)
Specificity of hinterworld: 0.019
Most over-linked city: Washington DC (0.061)
Most under-linked city: Athens (-0.038)
Specificity of hinterworld: 0.017
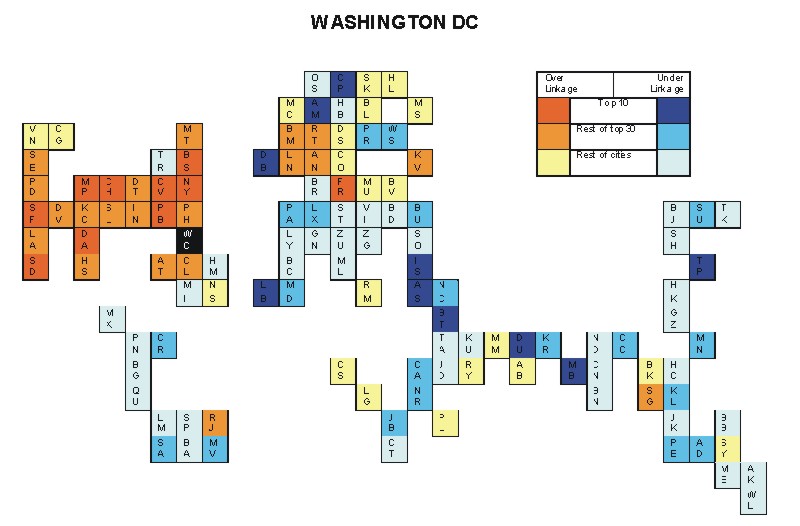
Most over-linked city: Washington, DC (0.071)
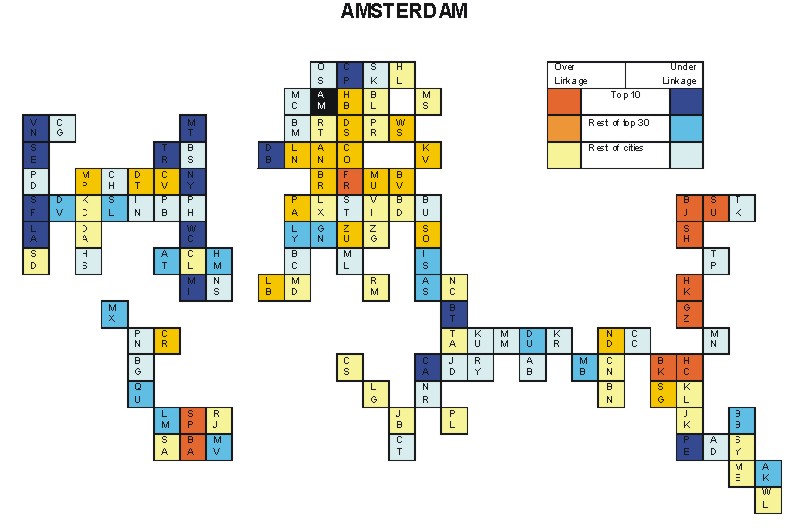
Most under-linked city: Amsterdam (-0.043)
Specificity of hinterworld: 0.021
Most over-linked city: Berlin (0.099)
Most under-linked city: New York (-0.080)
Specificity of hinterworld: 0.035

Most over-linked city: Hamburg (0.104)
Most under-linked city: Ho Chi Minh City (-0.097)
Specificity of hinterworld: 0.042
Most over-linked city: Milan (0.036)
Most under-linked city: Vancouver (-0.037)
Specificity of hinterworld: 0.013
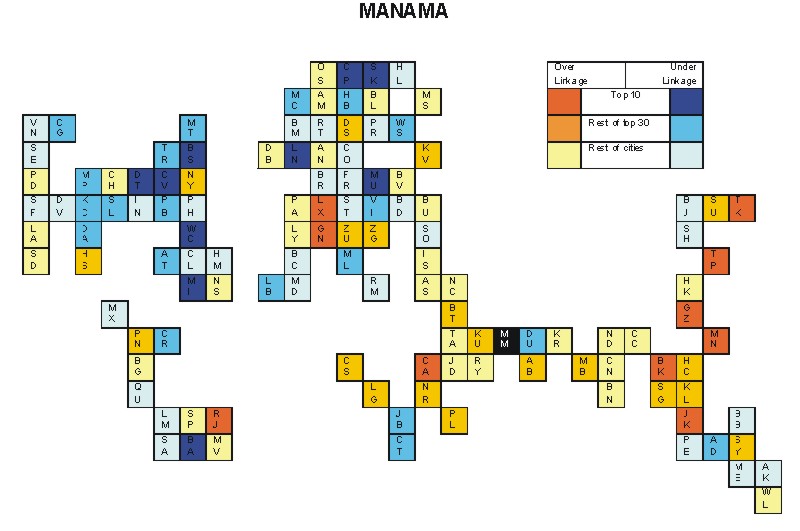
Most over-linked city: Jakarta (0.097)
Most under-linked city: Miami (-0.078)
Specificity of hinterworld: 0.038
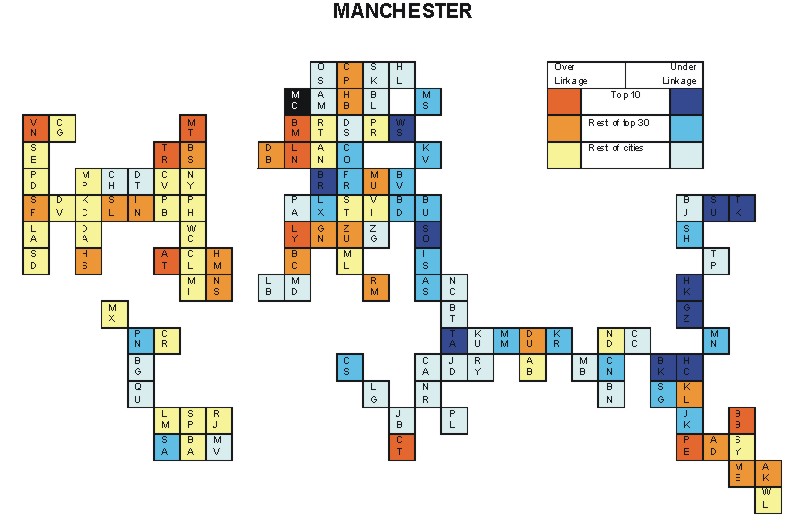
Most over-linked city: Birmingham (0.126)
Most under-linked city: Guangzhou (-0.087)
Specificity of hinterworld: 0.043
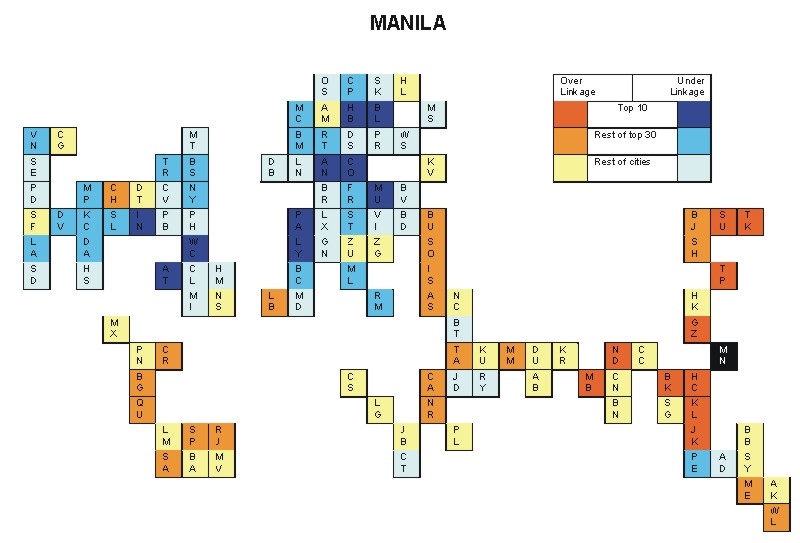
Most over-linked city: Bangkok (0.077)
Most under-linked city: Munich (-0.061)
Specificity of hinterworld: 0.025
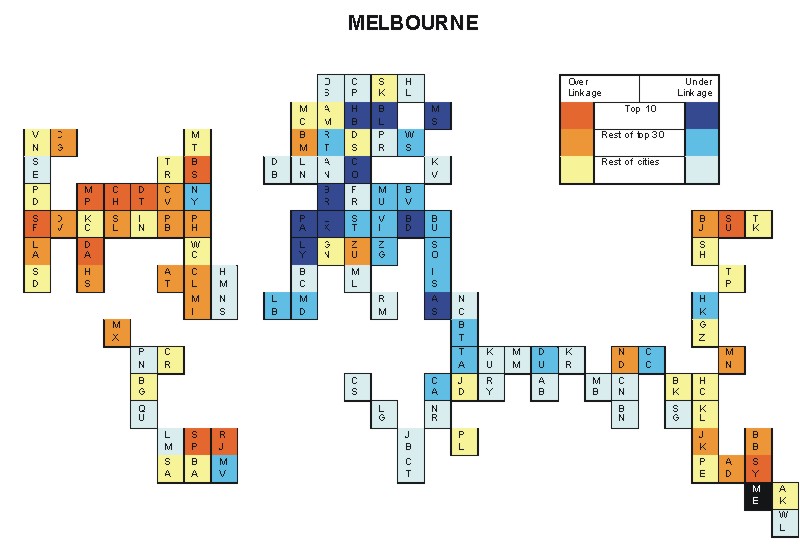
Most over-linked city: Chicago (0.057)
Most under-linked city: Lyon (-0.038)
Specificity of hinterworld: 0.020

Most over-linked city: Seoul (0.039)
Most under-linked city: Barcelona (-0.044)
Specificity of hinterworld: 0.015

Most over-linked city: Dallas (0.0.049)
Most under-linked city: Kuala Lumpur (-0.036)
Specificity of hinterworld: 0.020
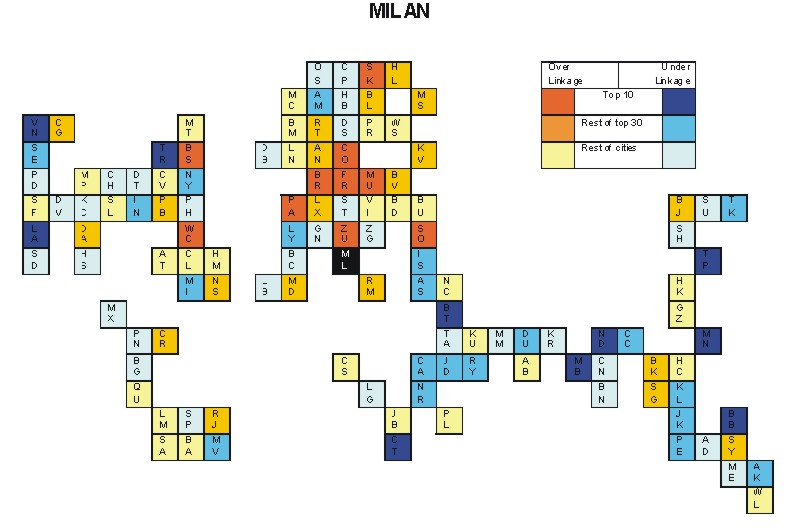
Most over-linked city: Frankfurt (0.039)
Most under-linked city: Los Angeles (-0.044)
Specificity of hinterworld: 0.014

Most over-linked city: Charlotte (0.121)
Most under-linked city: Tel Aviv (-0.077)
Specificity of hinterworld: 0.045
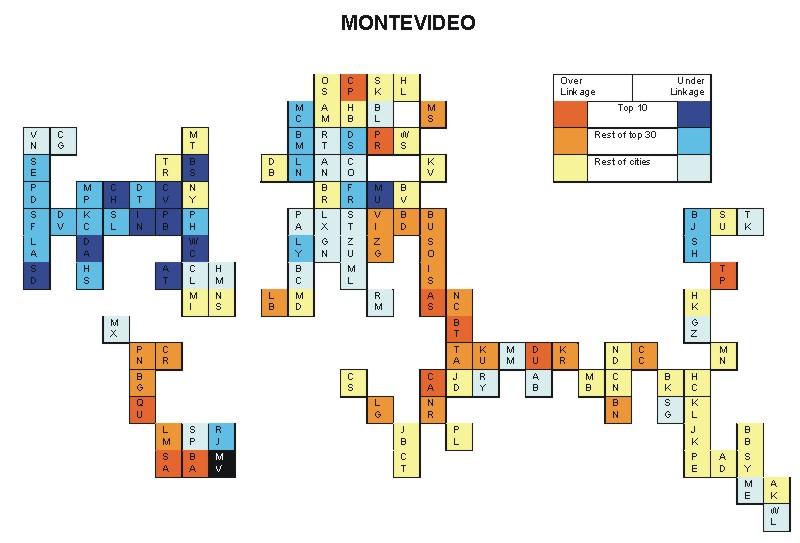
Most over-linked city: Santiago (0.096)
Most under-linked city: Washington, DC (-0.120)
Specificity of hinterworld: 0.039
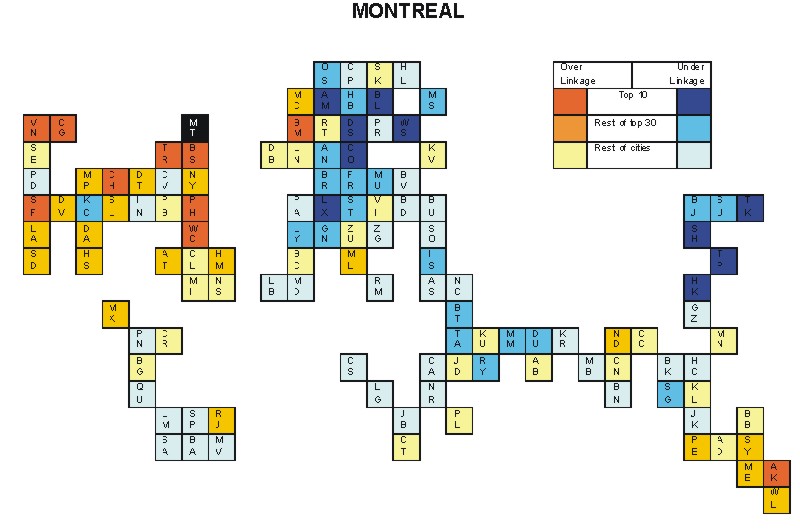
Most over-linked city: Boston (0.069)
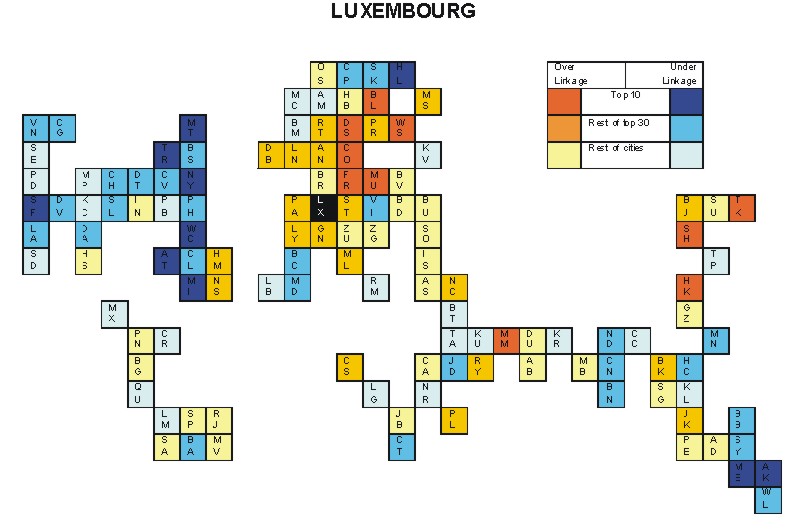
Most under-linked city: Luxembourg (-0.074)
Specificity of hinterworld: 0.028
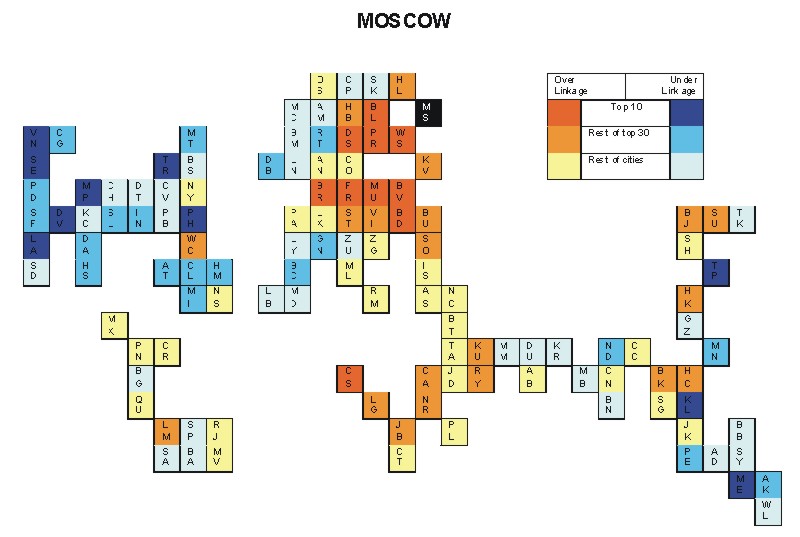
Most over-linked city: Budapest (0.070)
Most under-linked city: Los Angeles (-0.043)
Specificity of hinterworld: 0.023
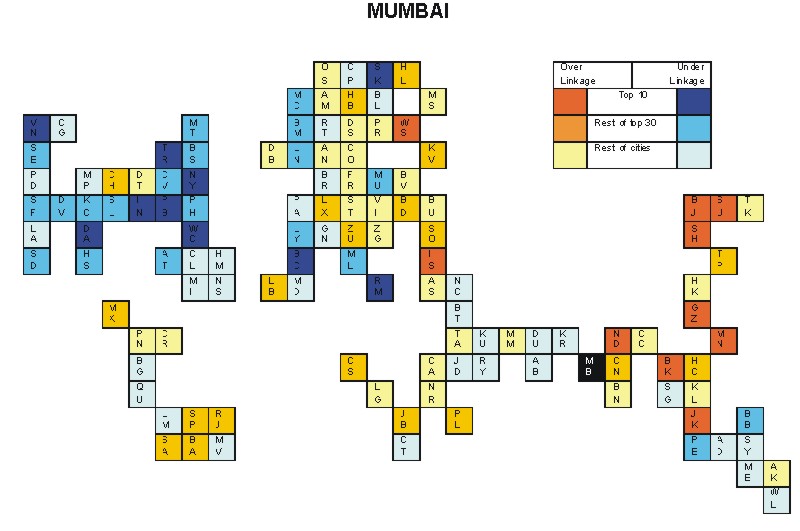
Most over-linked city: Shanghai (0.050)
Most under-linked city: Stockholm (-0.037)
Specificity of hinterworld: 0.019
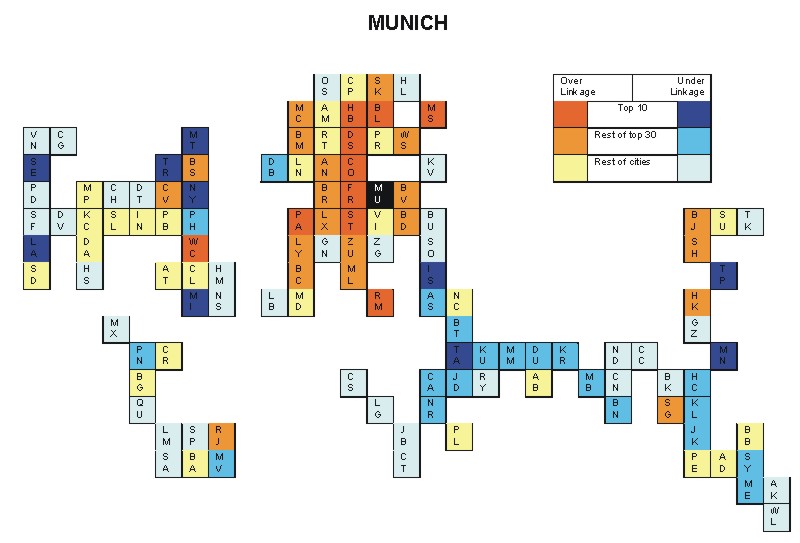
Most over-linked city: Berlin (0.140)
Most under-linked city: Manila (-0.071)
Specificity of hinterworld: 0.037
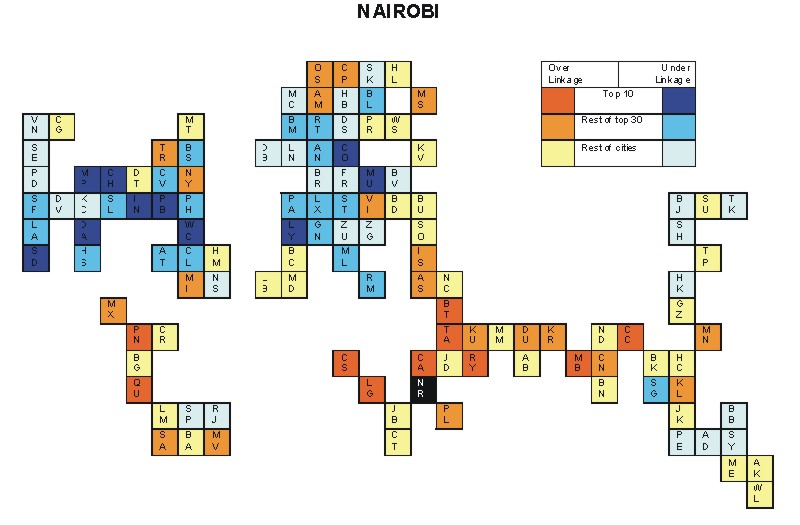
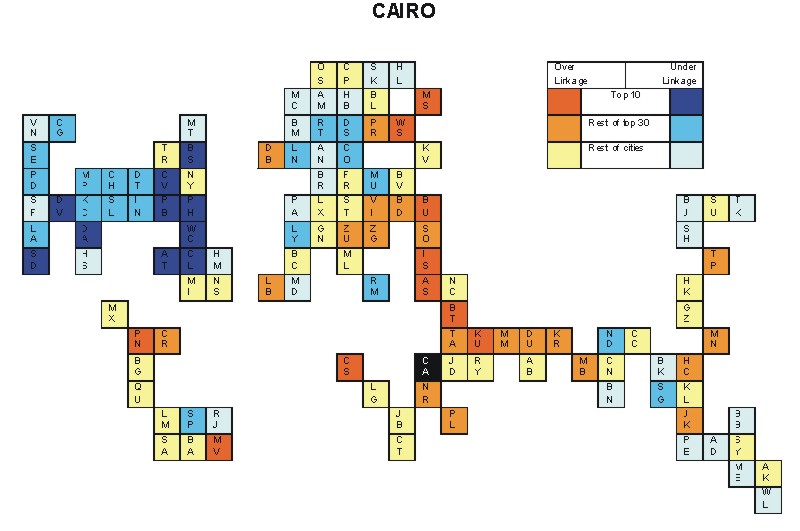
Most over-linked city: Cairo (0.099)
Most under-linked city: Washington, DC (-0.107)
Specificity of hinterworld: 0.046
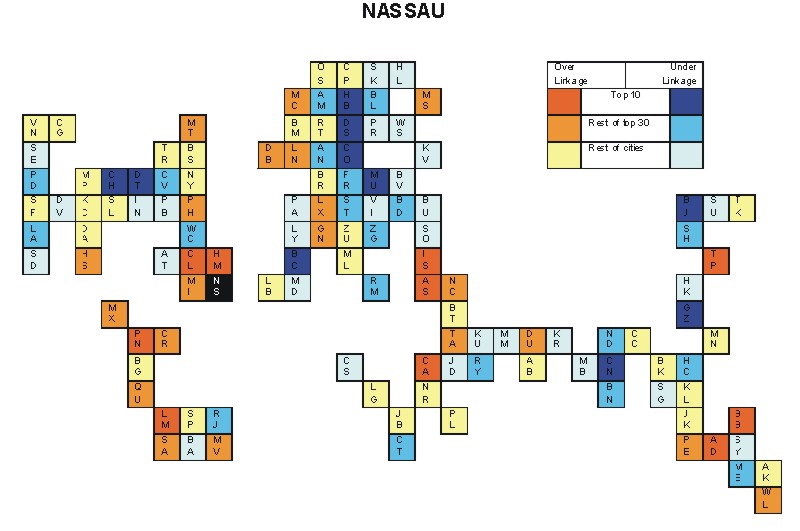
Most over-linked city: Lima (0.073)
Most under-linked city: Dusseldorf (-0.114)
Specificity of hinterworld: 0.036

Most over-linked city: Chicago (0.073)
Most under-linked city: Beirut (-0.039)
Specificity of hinterworld: 0.022
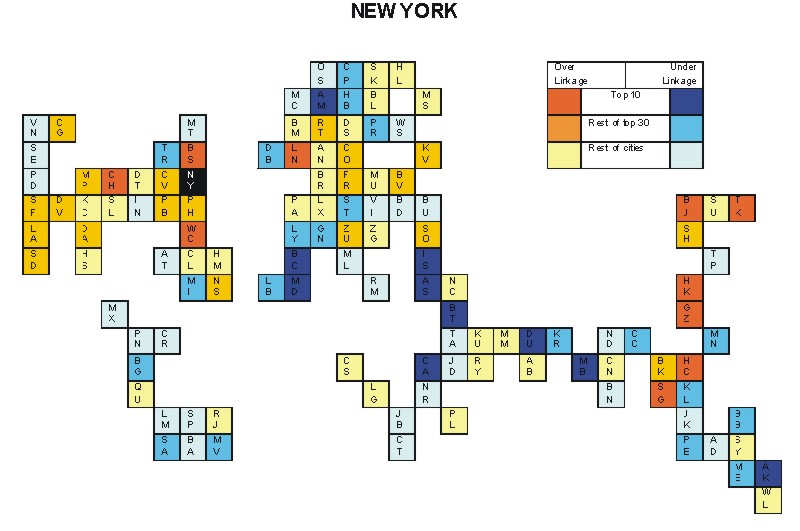
Most over-linked city: Washington DC (0.062)
Most under-linked city: Athens (-0.036)
Specificity of hinterworld: 0.018
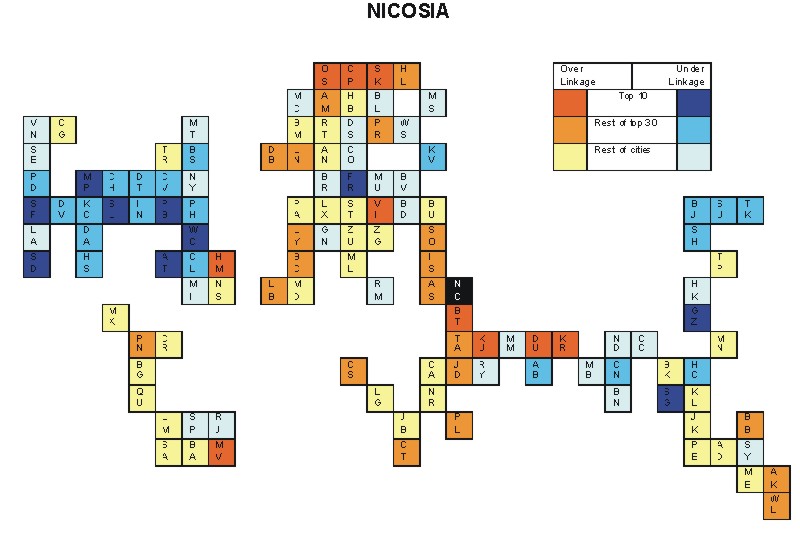
Most over-linked city: Copenhagen (0.117)
Most under-linked city: Frankfurt (-0.114)
Specificity of hinterworld: 0.048
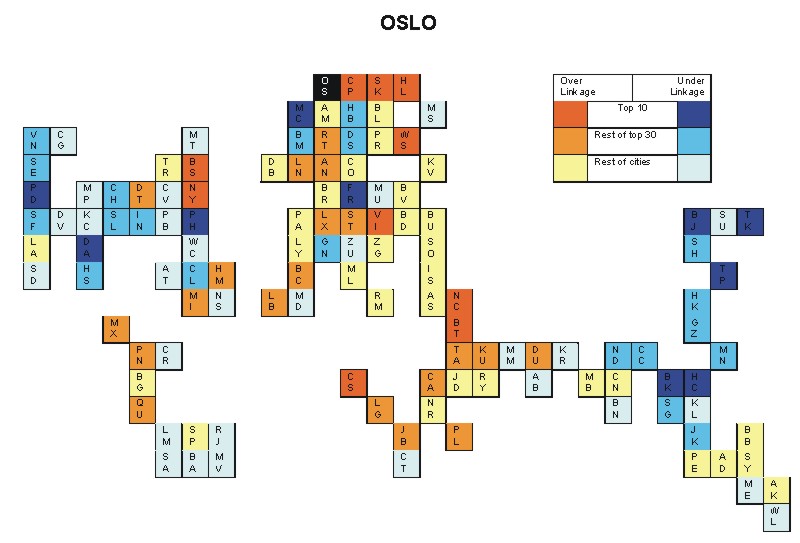
Most over-linked city: Copenhagen (0.116)
Most under-linked city: Portland (-0.071)
Specificity of hinterworld: 0.029
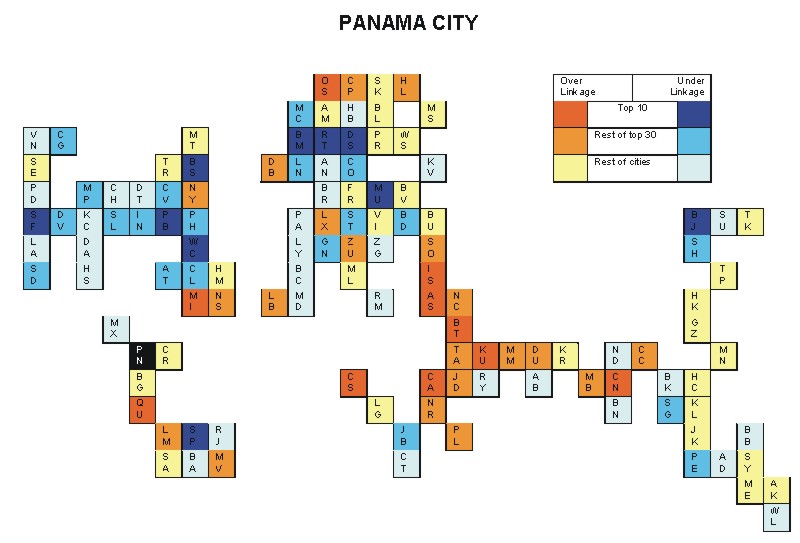
Most over-linked city: Quito (0.081)
Most under-linked city: Washington, DC (-0.086)
Specificity of hinterworld: 0.034

Most over-linked city: Frankfurt (0.037)
Most under-linked city: Auckland (-0.032)
Specificity of hinterworld: 0.015
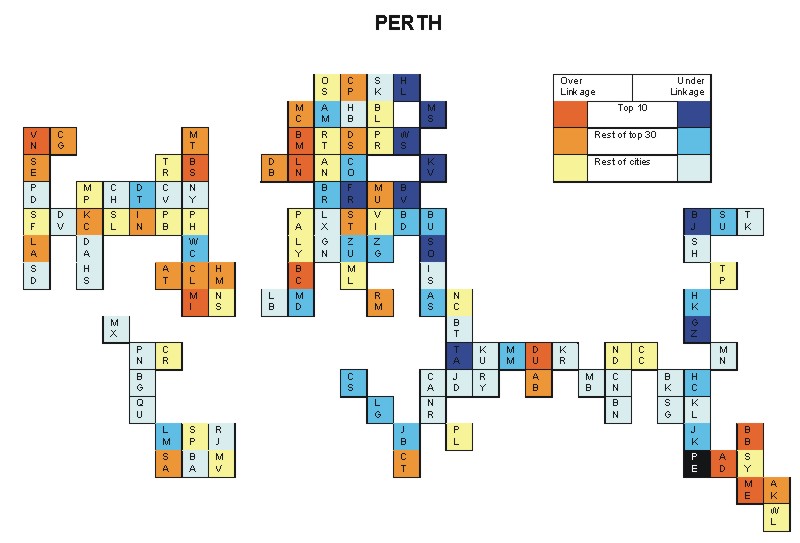
Most over-linked city: Adelaide (0.146)
Most under-linked city: Sofia (-0.081)
Specificity of hinterworld: 0.038
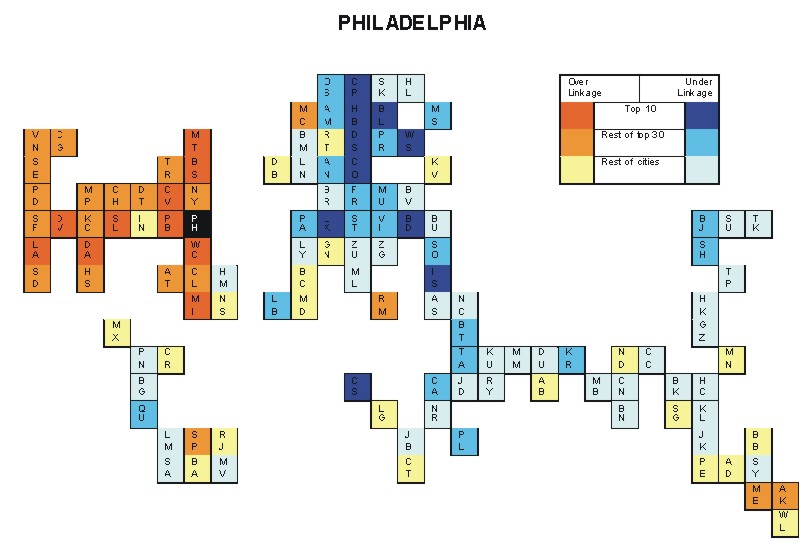
Most over-linked city: Dallas (0.120)
Most under-linked city: Dusseldorf (-0.076)
Specificity of hinterworld: 0.044

Most over-linked city: Washington, DC (0.176)
Most under-linked city: Istanbul (-0.097)
Specificity of hinterworld: 0.061
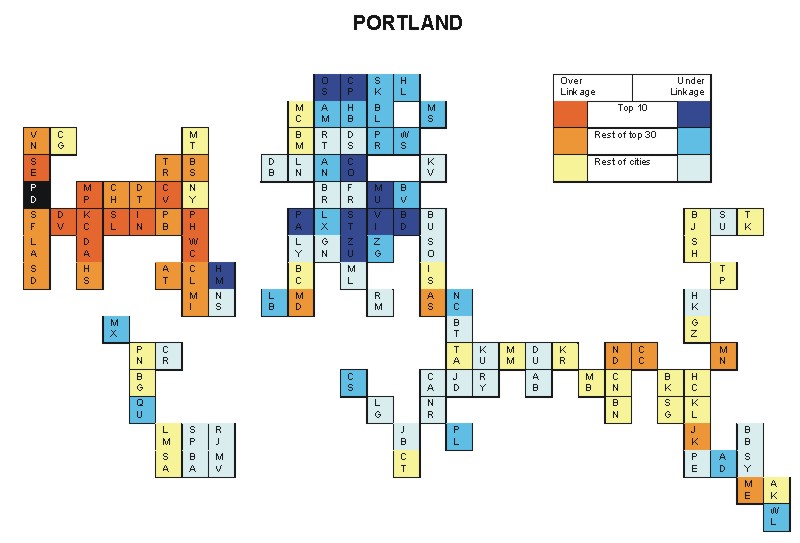
Most over-linked city: Seattle (0.160)
Most under-linked city: Copenhagen (-0.116)
Specificity of hinterworld: 0.049

Most over-linked city: Hamilton (0.077)
Most under-linked city: Philadelphia (-0.082)
Specificity of hinterworld: 0.034

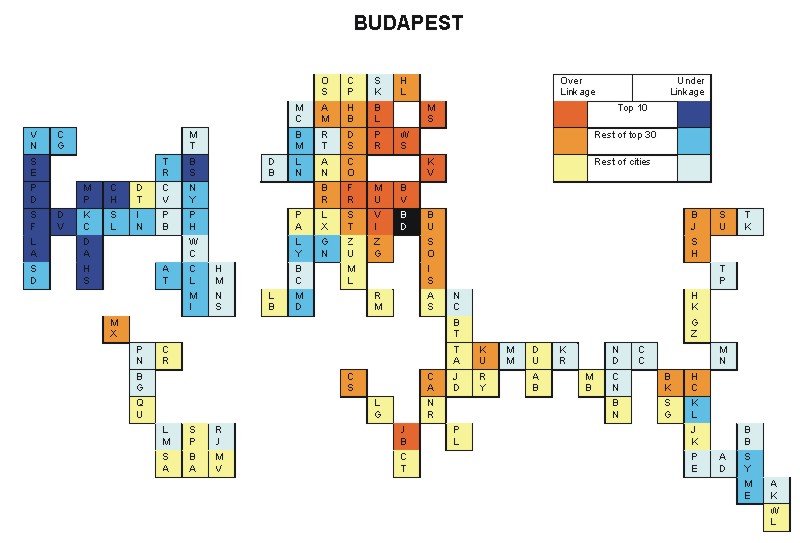
Most over-linked city: Budapest (0.092)
Most under-linked city: Los Angeles (-0.064)
Specificity of hinterworld: 0.028

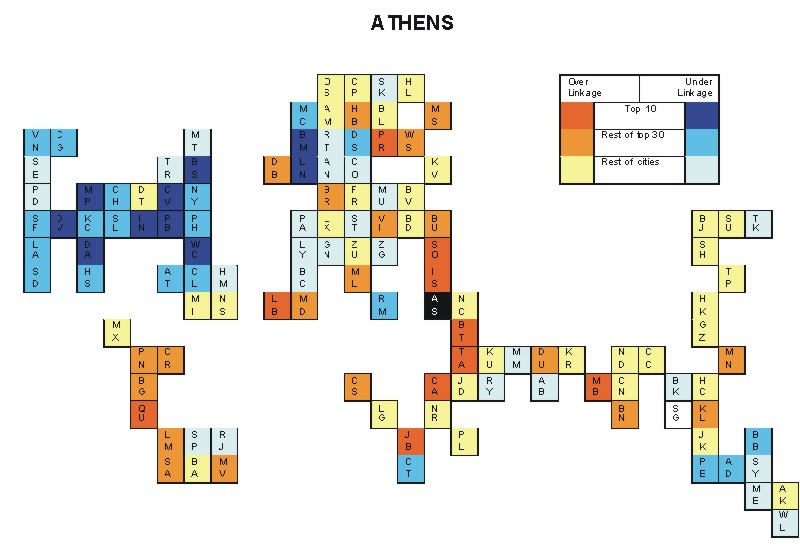
Most over-linked city: Athens (0.110)
Most under-linked city: Chicago (-0.105)
Specificity of hinterworld: 0.045
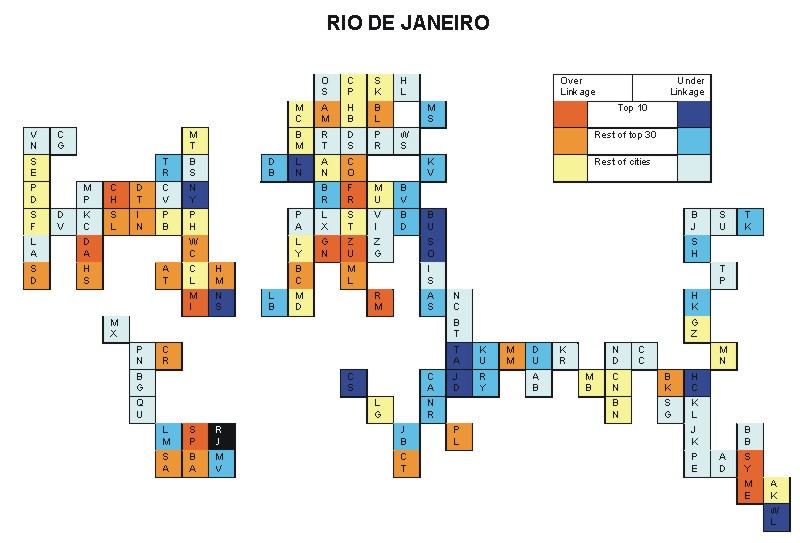
Most over-linked city: Zurich (0.062)
Most under-linked city: New York (-0.048)
Specificity of hinterworld: 0.022

Most over-linked city: Casablanca (0.069)
Most under-linked city: Singapore (-0.072)
Specificity of hinterworld: 0.026
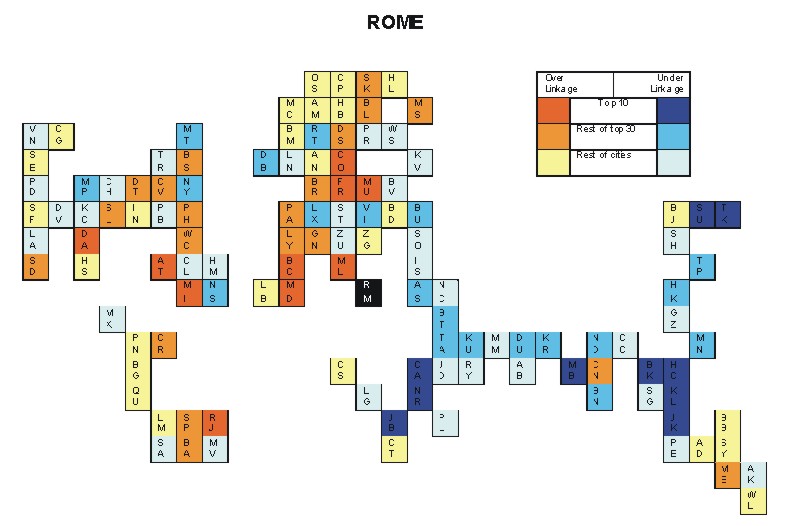
Most over-linked city: Munich (0.058)
Most under-linked city: Tokyo (-0.048)
Specificity of hinterworld: 0.022
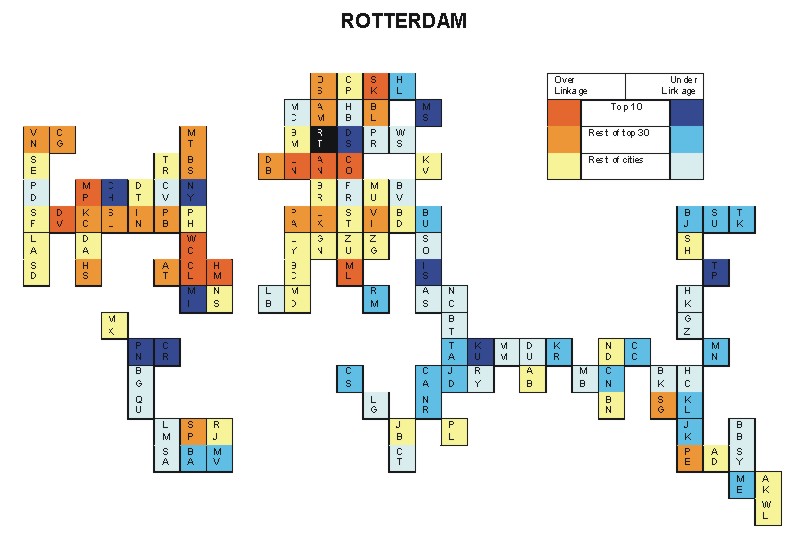
Most over-linked city: London (0.089)
Most under-linked city: Taipei (-0.064)
Specificity of hinterworld: 0.032
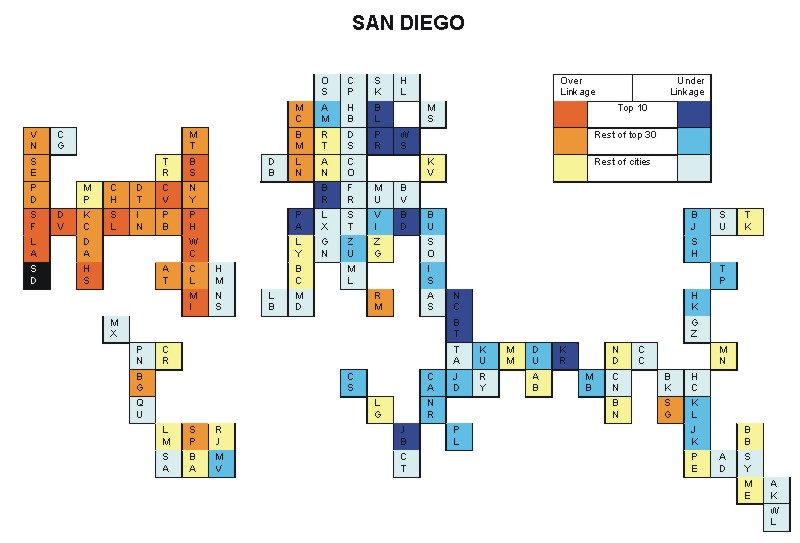
Most over-linked city: Washington, DC (0.193)
Most under-linked city: Prague (-0.094)
Specificity of hinterworld: 0.050
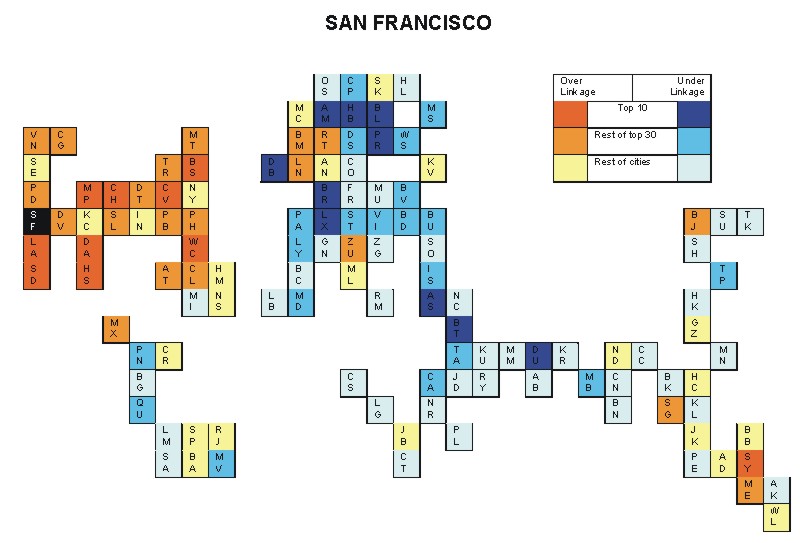
Most over-linked city: Boston ( 0.086)
Most under-linked city: Amsterdam (-0.044)
Specificity of hinterworld: 0.024
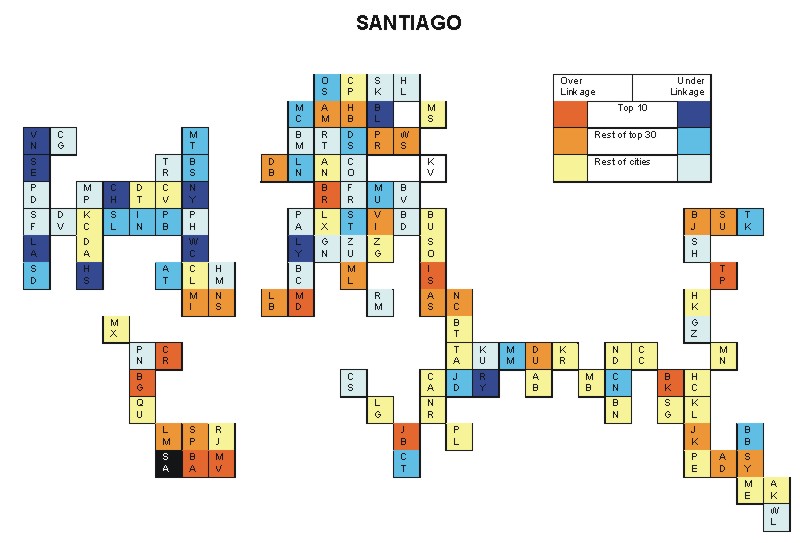
Most over-linked city: Caracas (0.079)
Most under-linked city: New York (-0.045)
Specificity of hinterworld: 0.022

Most over-linked city: Bangkok (0.047)
Most under-linked city: Copenhagen (-0.033)
Specificity of hinterworld: 0.015
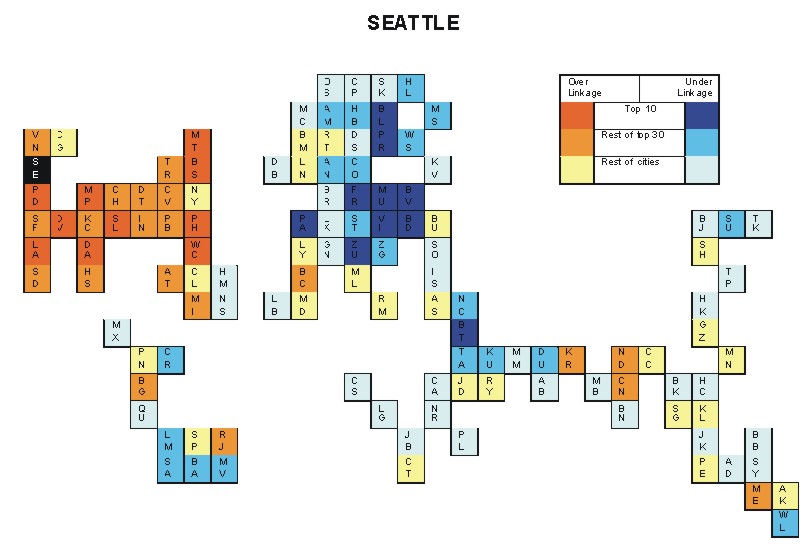
Most over-linked city: Dallas (0.117)
Most under-linked city: Munich (-0.079)
Specificity of hinterworld: 0.039

Most over-linked city: Beijing (0.068)
Most under-linked city: Barcelona (-0.063)
Specificity of hinterworld: 0.023
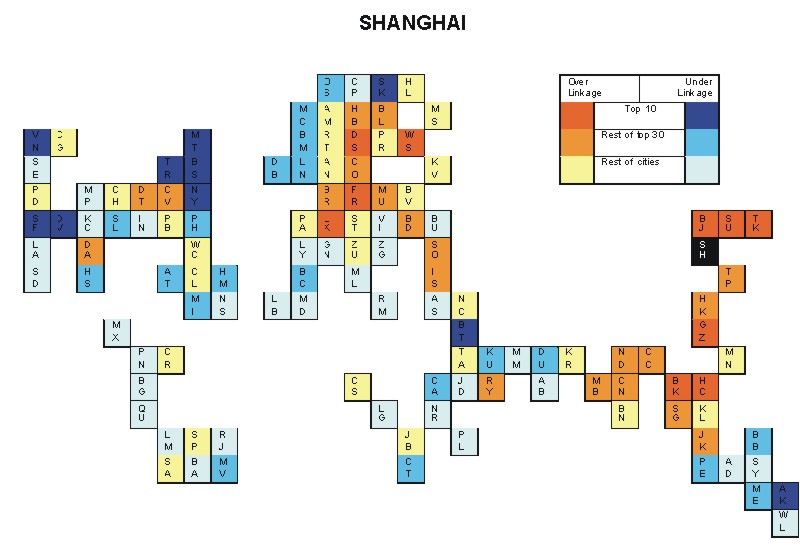
Most over-linked city: Guangzhou (0.074)
Most under-linked city: Toronto (-0.072)
Specificity of hinterworld: 0.025

Most over-linked city: Beijing (0.044)
Most under-linked city: Auckland (-0.039)
Specificity of hinterworld: 0.016
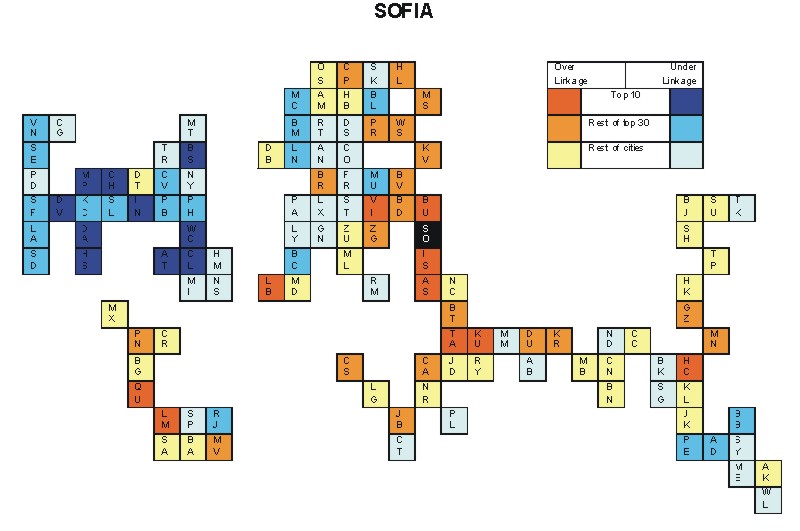
Most over-linked city: Athens (0.158)
Most under-linked city: Boston (-0.170)
Specificity of hinterworld: 0.064
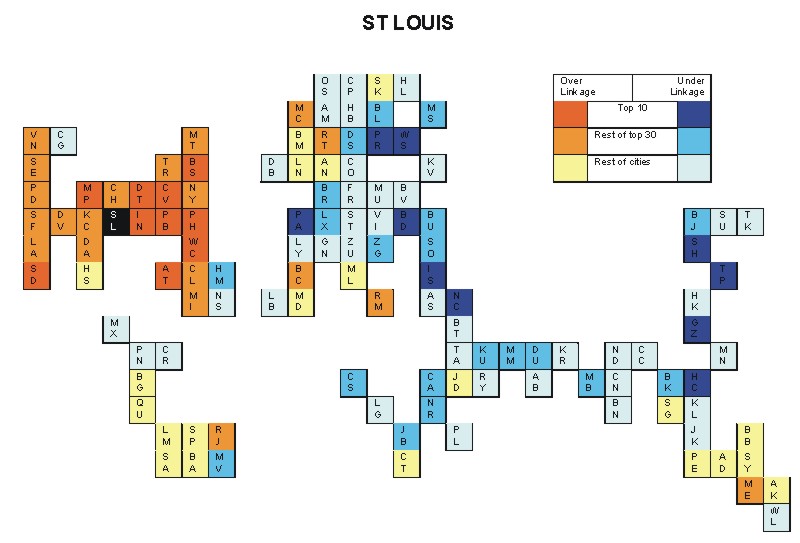
Most over-linked city: Washington, DC (0.141)
Most under-linked city: Warsaw (-0.086)
Specificity of hinterworld: 0.053
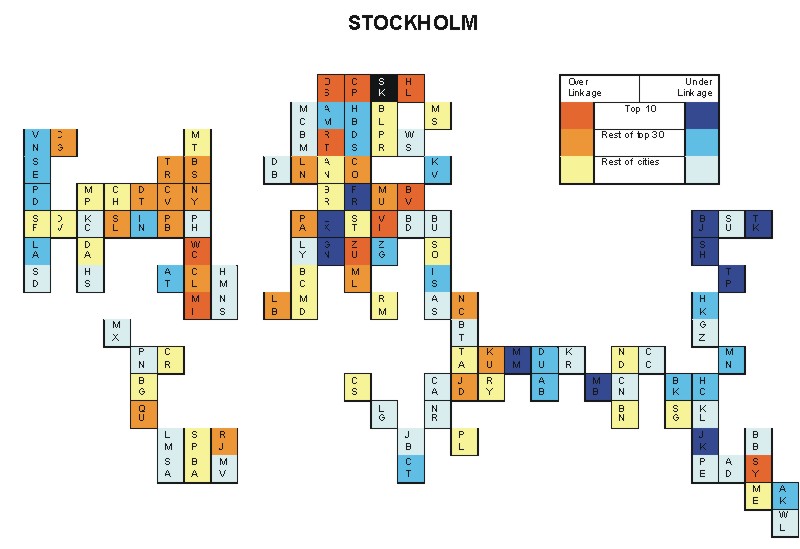
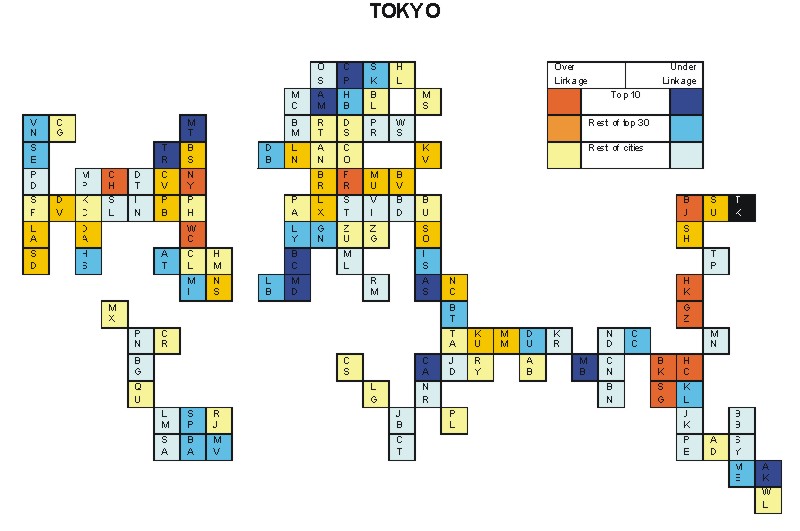
Most over-linked city: Copenhagen (0.048)
Most under-linked city: Tokyo (-0.056)
Specificity of hinterworld: 0.018
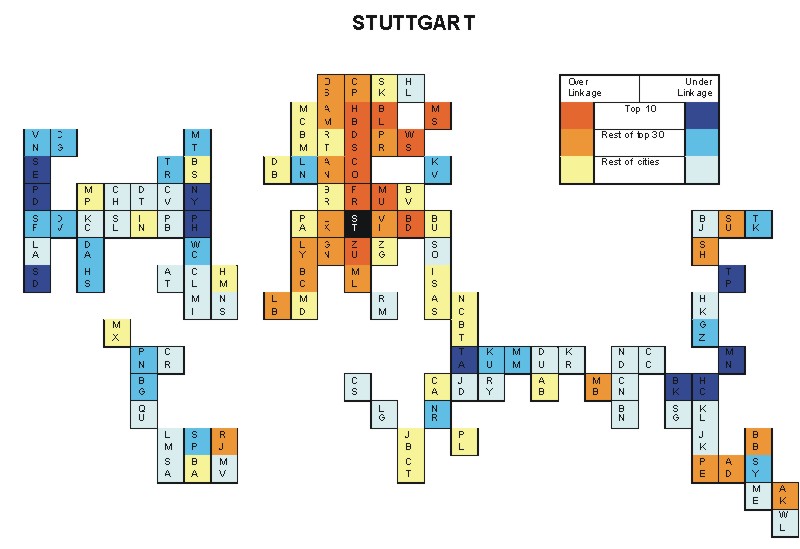
Most over-linked city: Munich (0.214)
Most under-linked city: New York (-0.097)
Specificity of hinterworld: 0.045
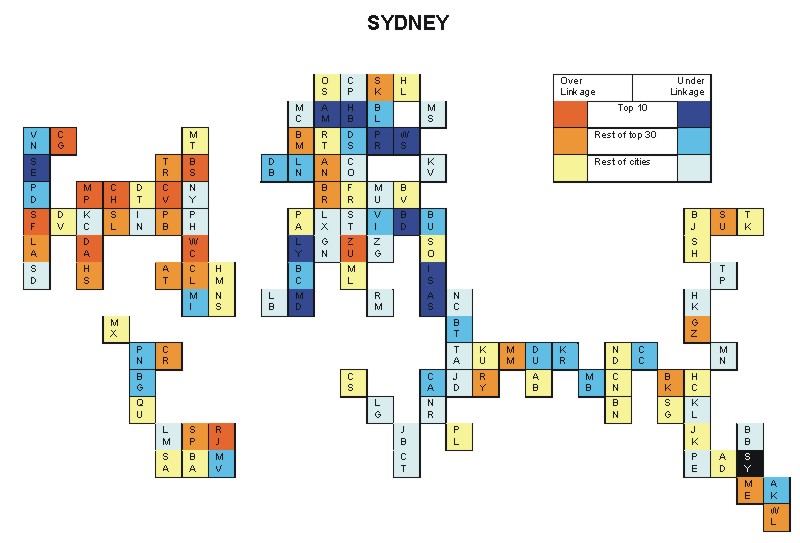
Most over-linked city: Chicago (0.049)
Most under-linked city: Hamburg (-0.034)
Specificity of hinterworld: 0.015
Most over-linked city: Bangkok (0.087)
Most under-linked city: Boston (-0.050)
Specificity of hinterworld: 0.024
Most over-linked city: Sofia (0.119)
Most under-linked city: Munich (-0.145)
Specificity of hinterworld: 0.055
Most over-linked city: Washington, DC (0.046)
Most under-linked city: Toronto (-0.048)
Specificity of hinterworld: 0.017

Most over-linked city: Boston (0.052)
Most under-linked city: Berlin (-0.038)
Specificity of hinterworld: 0.015
Most over-linked city: Montreal (0.095)
Most under-linked city: Frankfurt (-0.099)
Specificity of hinterworld: 0.036
Most over-linked city: Helsinki (0.061)
Most under-linked city: Dallas (-0.043)
Specificity of hinterworld: 0.023
Most over-linked city: Budapest (0.072)
Most under-linked city: Los Angeles (-0.069)
Specificity of hinterworld: 0.030
Most over-linked city: Chicago (0.079)
Most under-linked city: Dubai (-0.069)
Specificity of hinterworld: 0.027
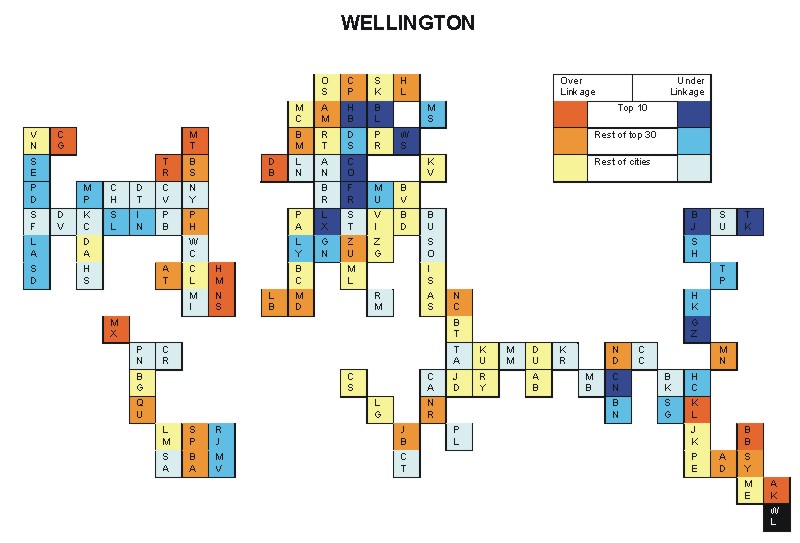
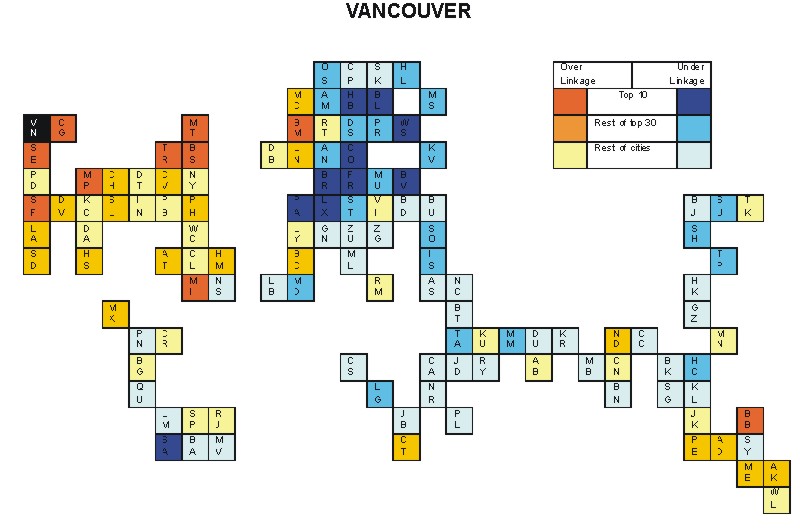
Most over-linked city: Auckland (0.070)
Most under-linked city: Frankfurt (-0.080)
Specificity of hinterworld: 0.028
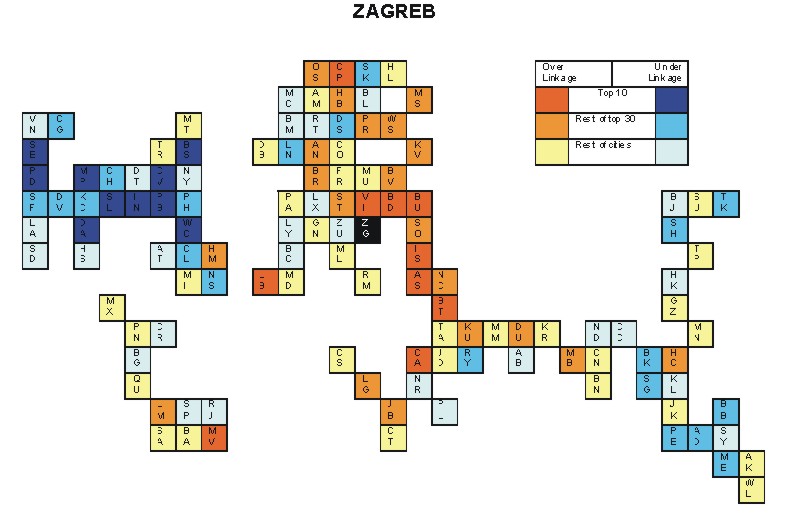
Most over-linked city: Budapest (0.096)
Most under-linked city: Washington, DC (-0.119)
Specificity of hinterworld: 0.047

Most over-linked city: Chicago (0.040)
Most under-linked city: Seattle (-0.034)
Specificity of hinterworld: 0.014
City codes
AB Abu Dhabi; AD Adelaide; AK Auckland; AM Amsterdam; AS Athens; AT Atlanta; AN Antwerp; BA Buenos Aires; BB Brisbane; BC Barcelona; BD Budapest; BG Bogota; BJ Beijing; BK Bangkok; BL Berlin; BM Birmingham; BN Bangalore; BR Brussels; BS Boston; BT Beirut; BU Bucharest; BV Bratislava; CA Cairo; CC Calcutta; CG Calgary; CH Chicago; CL Charlotte; CN Chennai; CO Cologne; CP Copenhagen; CR Caracas; CS Casablanca; CT Cape Town; CV Cleveland; DA Dallas; DB Dublin; DS Dusseldorf; DT Detroit; DU Dubai; DV Denver; FR Frankfurt; GN Geneva; GZ Guangzhou; HB Hamburg; HC Ho Chi Minh City; HK Hong Kong; HL Helsinki; HM Hamilton(Bermuda); HS Houston; IN Indianapolis; IS Istanbul; JB Johannesburg; JD Jeddah; JK Jakarta; KC Kansas City; KL Kuala Lumpur; KR Karachi; KU Kuwait; KV Kiev; LA Los Angeles; LB Lisbon; LG Lagos; LM Lima; LN London; LX Luxembourg; LY Lyon; MB Mumbai; MC Manchester; MD Madrid; ME Melbourne; MI Miami; ML Milan; MM Manama; MN Manila; MP Minneapolis; MS Moscow; MT Montreal; MU Munich; MV Montevideo; MX Mexico City; NC Nicosia; ND New Delhi; NR Nairobi; NS Nassau; NY New York; OS Oslo; PA Paris; PB Pittsburgh; PD Portland; PE Perth; PH Philadelphia; PL Port Louis; PN Panama City; PR Prague; QU Quito; RJ Rio de Janeiro; RM Rome; RT Rotterdam; RY Riyadh; SA Santiago; SD San Diego; SE Seattle; SF San Francisco; SG Singapore; SH Shanghai; SK Stockholm; SL St Louis; SO Sofia; SP Sao Paulo; ST Stuttgart; SU Seoul; SY Sydney; TA Tel Aviv; TP Taipei; TR Toronto; TY Tokyo; VI Vienna; VN Vancouver; WC Washington DC; WL Wellington; WS Warsaw; ZG Zagreb; ZU Zurich (see also map of city codes below).